The space obtained by identifying the antipodal points of a circle

Question

Take the unit circle $S^1$ in $\Bbb{R}^2$ and partition it into subsets which contain exactly two points, the points being antipodal (at opposite ends of a diameter). $P$ is the resulting identification space.

Now, what is homeomorphic to $P$? My intuition says that it must be a semicircle. But couldn't construct a homeomorphism.

The set consisting of points of the upper/lower half of the unit circle — Xena, Jul 01 '13 at 19:38
Should we consider this a duplicate of http://math.stackexchange.com/q/298879/264 ? — Zev Chonoles, Jul 01 '13 at 19:39
Topologically, it's a circle, BUT when you do this with the $2$-sphere, the quotient space is not another $2$-spere, but a non-orientable surface: the projective plane. — Michael Hardy, Jul 01 '13 at 19:49
The space you describe arises naturally as the domain of the trigonometric tangent function $tan$, and I thought this was some sort of exotic space, but the answers on this page reveal it's just the topological circle, again... — étale-cohomology, May 19 '17 at 09:35

Zev Chonoles · Accepted Answer · 2013-07-05T21:56:05.180

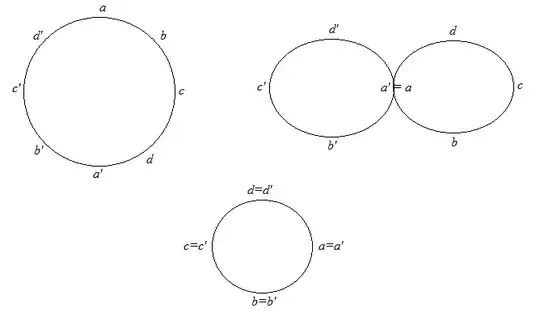
Identify antipodal points on the circle:

enter image description here

Form the identification space:

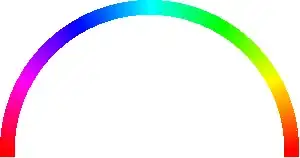
enter image description here

Moving along this space, you come back to where you started... just like on a circle:

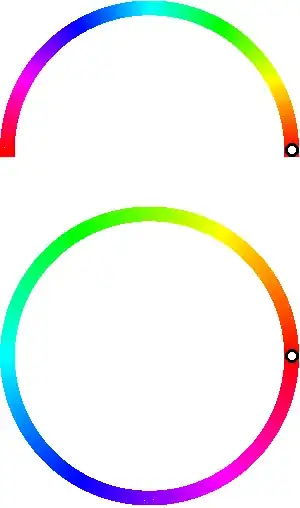
enter image description here

(original gifs here and here; I joined them because when they load at different times in the browser, they don't stay in sync)

This correspondence between the points of $P$ and the points of $S^1$ is a homeomorphism.

PlotUpTo[angle_, colorscale_] := 
 ParametricPlot[{Cos[t], Sin[t]}, {t, 0, angle}, PlotStyle -> Thickness[0.05],
 ColorFunctionScaling -> False,
 ColorFunction -> Function[{x, y}, Hue[colorscale (Arg[-x - I y] + Pi)/(2 Pi )]],
 PlotRange -> All, PlotRangeClipping -> False, ImageSize -> {300}, Axes -> None]

AnimatedMarker[time_, speed_] := Graphics[{PointSize[0.05], 
 Point[{Cos[speed 2 Pi time], Sin[speed 2 Pi time]}],
 White, PointSize[0.03], Point[{Cos[speed 2 Pi time], Sin[speed 2 Pi time]}]}]

AnimatedPlot[angle_, colorscale_, time_, speed_] := 
 Show[PlotUpTo[angle, colorscale], AnimatedMarker[time, speed]]

Export["animation.gif", Table[Rasterize[
 TableForm[{{AnimatedPlot[Pi, 2, t, 1/2]}, {AnimatedPlot[2 Pi, 1, t, 1]}},
 TableSpacing -> {10, 0}]], {t, 0, 1, 0.01}], "DisplayDurations" -> {0.04}]

score 20 · Answer 2 · answered Jul 01 '13 at 19:46

20

Start with $S^1$, as in the first figure below. Hold it at $c'$ and $c$, and flip the righthand side over to form an $\infty$ sign, as in the second figure. Now fold the loops together into a single loop, as in the third figure. Everything matches up properly to give you your quotient space: it’s $S^1$ again.

enter image description here

answered Jul 01 '13 at 19:46

Brian M. Scott

631,399

Prof. Scott Is it possible to do something similar with $S^2$ (two-sphere)? – JanG May 05 '23 at 18:38
@JanG: Not really. The resulting object is the real projective plane, a non-orientable surface that cannot be embedded in $\Bbb R^3$. – Brian M. Scott May 05 '23 at 19:36
Thanks for your answer and the very useful link. – JanG May 06 '23 at 12:22
Prof. Scott Would you mind to look on my new question https://math.stackexchange.com/q/4693707/1003573? – JanG May 06 '23 at 16:20
@JanG: I looked, but I’m afraid that I can’t be of any help with that: it’s in an area about which I know virtually nothing. – Brian M. Scott May 06 '23 at 18:13
1

That's OK, thanks anyway! – JanG May 06 '23 at 18:59

score 10 · Answer 3 · answered Jul 01 '13 at 19:39

Consider the (complex) function $f(z) = z^2$ from the circle onto itself (seeing the plane as the complex plane). This identifies exactly the antipodal points on the circle. So this map induces a homeomporphism between $S^1$ modulo this equivalence and $S^1$.

score 7 · Answer 4 · answered Jul 01 '13 at 21:17

I think your space is homeomorphic to the real projective line $\mathbb{R}P^1$.

$\mathbb{R}P^1$ is space of one dimensional subspaces of $\mathbb{R}^2$. Look at wiki page, as you can see real projective line is homeomorphic to $S^1$. So what you get after your construction is circle again.

In fact if you do your construction in more dimensions. Take $S^n$ and glue antipodal points and you get $\mathbb{R}P^n$. But for example in two dimensions $\mathbb{R}P^2$ is not homeomorphic to sphere since real projective plane has genus 1.

The space obtained by identifying the antipodal points of a circle

4 Answers4

Linked

Related