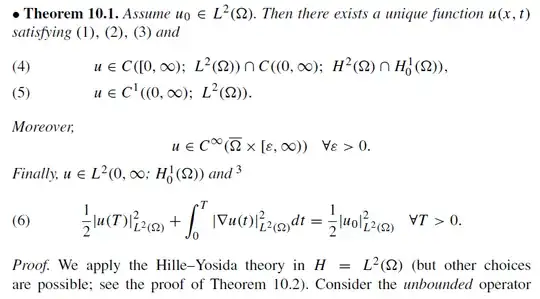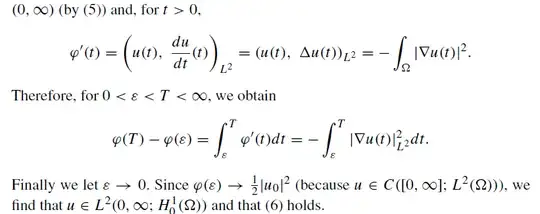I am reading the heat equation in Functional Analysis, Sobolev Spaces, and Partial Differential Equations by Haim Brezis, and having some concerns about the proof, whose screenshot is as attached below.
The notation $u\in L^2 (0, \infty; H^1_0(\Omega))$
I can't find the definition of the notation in the book, but I believe it means $$ \int_0^\infty \left\Vert u(t) \right\Vert ^2 _{H^1_0(\Omega)} dt < \infty$$ On $H^1_0(\Omega)$, $\left\Vert \nabla u(t) \right\Vert _{L^2(\Omega)} $ and $\left\Vert u(t) \right\Vert _{H^1(\Omega)} $ are equivalent norms by Poincare inequality.The boundary condition has been incorporated in the definition of the domain of A.
I think the key is $H_0^1(\Omega)$ since for a function $g\in H_0^1(\Omega)$ that admits a continuous representative, $g$ vanishes on the boundary. From the definition of domain $D(A) = H^2(\Omega) \cap H^1_0(\Omega)$, does it imply $g\in D(A)$ has a continuous representative? I believe the answer is no.$D(A^l) = \{g\in H^{2l}(\Omega); g = \Delta g = ... = \Delta^{l-1}g = 0 \text{ on the boundary} \}$
I can see $D(A^l) \subset H^{2l}(\Omega)$. The argument ($l = 2$ as an example) goes as follows.
$$ g \in D(A^2) \Rightarrow g \in D(A), - \Delta g \in D(A) \Rightarrow - \Delta g + g \in H^2(\Omega) \Rightarrow g \in H^4(\Omega)$$
The last arrow follows from a regularity theorem (Theorem 9.25). But again, $g\in D(A^l)$ may not have a continuous representative (at least when $l$ is not sufficiently large) so how to see $g = \Delta g =... = 0$ on the boundary?$u\in C^k((0,\infty); C^k(\bar \Omega))$ for all k
My understanding is that $u$ as a function from $(0,\infty)$ to $C^k(\bar \Omega)$ is a $C^k$ function, and for each fixed $t_1$, $u(t_1)$ is a $C^k$ function on $\bar \Omega$. How do we conclude from here that $u(x,t): \Omega \times (0, \infty) \to \mathbb{R}$ is $C^k$? The differentiability of $u\in C^k((0,\infty); C^k(\bar \Omega))$ uses the Banach space topology while the partial derivative $u_t(x,t)$ in $t$ is formulated in the usual sense.
More specifically, let $[U(t)](x)$ be the map viewed as $(0,\infty)$ to $C^k(\bar \Omega)$ and $u(x,t)$ be the one viewed as $\Omega \times (0,\infty) \to \mathbb{R}$, how to show that $u_t(x,t) = d[U(t)](x)/dt $?
(Update)
I consulted Evan's PDE book, and my own answers (at least how I convinced myself) go as follows.
- For point 1, yes. More generally, $u\in L^p(0,\infty; X)$ for a Banach space $X$ means $$ \int_0^\infty \left\Vert u(t) \right\Vert ^ p _X dt < \infty $$
- For point 2 & 3, we need the fact that $$ u \in H^1_0 (\Omega) \iff u = 0 \text{ on the boundary}$$To justify the statement (since $u$ can differ from a set of measure zero and the boundary has measure zero), we probably need the theory of trace. Anyways, in Brezis' book, only a special case is proven (when $u$ has a continuous representative, see Theorem 9.17), and the trace operator is briefly mentioned in page 315.
- I think I came up with a solution for point 4.
Let $u(x,t) = [U(t)](x)$. Fix a point $x_0 \in \Omega$. $$(\frac{d[U(t)]}{dt}) (x_0) = (\lim_{h\to 0}\frac{U(t+h)-U(t)}{h})(x_0) = \lim_{h\to 0}\frac{[U(t+h)](x_0)-[U(t)](x_0)}{h} = u_t(x_0,t)$$ since the continuity of evaluation at $x_0$ allows us to pass through the limit.
If there is any mistake or there is a better way/answer for my questions, please let me know. Anyways I hope this post helps those who only read Brezis' book like me.