Intersection of circle and geodesic segment on sphere

Question

I am trying to find an efficient way of computing the intersection point(s) of a circle and line segment on a spherical surface.

Say you have a sphere of radius R. On the surface of this sphere are

1. a circle with center ($\theta_c$,$\phi_c$) and radius r
2. a geodesic line segment defined by endpoints ($\theta_1$,$\phi_1$) and ($\theta_2$,$\phi_2$)

where $\theta$ is the colatitude in $[0,\pi]$, $\phi$ is the longitude in $[0,2\pi]$, and $r$ is measured by the geodesic distance on the sphere (not straight line distance in Euclidean space). How would you

1. determine whether the circle and line intersect at all, including whether the segment is contained by the circle?
2. compute the intersection point(s)?

We can assume there is nothing pathological going on. $r$ is not zero and is not so large that it's bigger than the sphere, the line's endpoints are not identical, etc.

Answer 1

If everything is converted from geographic coordinates to Cartesian vectors, the calculation can be done by linear algebra and trigonometry.

Let $P_{0}$ denote the center of the circle $C$; $P_{1}$ and $P_{2}$ the endpoints of the geodesic segment; and assume

• $P_{1} \neq \pm P_{2}$, so there is a unique short arc of great circle from $P_{1}$ to $P_{2}$;
• $r < \pi R/2$, so $C$ is not a great circle.

The great circle through $P_{1}$ and $P_{2}$ is the intersection of the sphere with the plane $\Pi$ containing $P_{1}$, $P_{2}$, and the origin (the center of the sphere), which has unit normal vector $$ N = \frac{P_{1} \times P_{2}}{\|P_{1} \times P_{2}\|}. $$ The angle subtended at the center of the sphere by the center of $C$ and a point of $C$ is $\theta = r/R$. Further, $\Pi$ intersects $C$ if and only if $N$ makes angle no larger than $\theta$ with the "equator" perpendicular to $P_{0}$, if and only if $$ \biggl|\frac{\pi}{2} - \arccos \frac{P_{0} \cdot N}{R}\biggr| = \biggl|\arcsin \frac{P_{0} \cdot N}{R}\biggr| \leq \theta. $$ If this inequality fails to hold, the plane $\Pi$ (and hence the geodesic segment) does not intersect $C$. If equality holds, $C$ is tangent to $\Pi$, and if strict inequality holds $C$ crosses $\Pi$.

Suppose the preceding inequality is satisfied. The Euclidean center of $C$ is $c_{0} = (\cos\theta)P_{0}$.

Let $P_{2}'$ denote the vector on the short arc starting at $P_{1}$ and heading toward $P_{2}$ that is perpendicular to $P_{1}$; namely, scale the orthogonal projection $$ P_{2} - \frac{P_{1} \cdot P_{2}}{R^{2}} P_{1} $$ to have magnitude $R$. Points on the great circle have the form $$ Q = (\cos t)P_{1} + (\sin t)P_{2}' $$ for some real $t$. Such a point lies on $C$ if and only if $(Q - c_{0}) \cdot P_{0} = 0$, or $$ (\cos t)P_{1} \cdot P_{0} + (\sin t)P_{2}' \cdot P_{0} = c_{0} \cdot P_{0} = R^{2}\cos\theta. $$ If we set $$ A = P_{1} \cdot P_{0},\qquad B = P_{2}' \cdot P_{0},\qquad C = R^{2}\cos \theta, $$ this equation is written $A\cos t + B\sin t = C$. To solve, let $t_{0} = \operatorname{atan2}(B, A)$ be the unique angle in $[0, 2\pi)$ satisfying $$ \cos t_{0} = \frac{A}{\sqrt{A^{2} + B^{2}}},\qquad \sin t_{0} = \frac{B}{\sqrt{A^{2} + B^{2}}}. $$ By the addition formula for cosine, we have $$ \cos(t - t_{0}) = \frac{R^{2}\cos\theta}{\sqrt{(P_{1} \cdot P_{0})^{2} + (P_{2}' \cdot P_{0})^{2}}}, $$ which yields $$ t = t_{0} \pm \arccos\frac{R^{2}\cos\theta}{\sqrt{(P_{1} \cdot P_{0})^{2} + (P_{2}' \cdot P_{0})^{2}}}. $$ This gives two points on the great circle that lie on $C$.

It remains to check whether either point lies on the short arc of great circle from $P_{1}$ to $P_{2}$. But $Q = (\cos t)P_{1} + (\sin t)P_{2}'$ lies on the arc of great circle from $P_{1}$ to $P_{2}$ if and only if $0 \leq t \leq \arccos(P_{1} \cdot P_{2}/R^{2})$. Alternatively, a point $Q$ of the great circle lies between $P_{1}$ and $P_{2}$ (i.e., on the short arc) if and on if the angle from $P_{1}$ to $Q$ plus the angle from $Q$ to $P_{2}$ equals the angle from $P_{1}$ to $P_{2}$, i.e., $$ \arccos \frac{P_{1} \cdot Q}{R^{2}} + \arccos \frac{P_{2} \cdot Q}{R^{2}} = \arccos \frac{P_{1} \cdot P_{2}}{R^{2}}. $$ (In the diagram, these were checked numerically and colored accordingly, green if yes and red if no.)

Answer 2

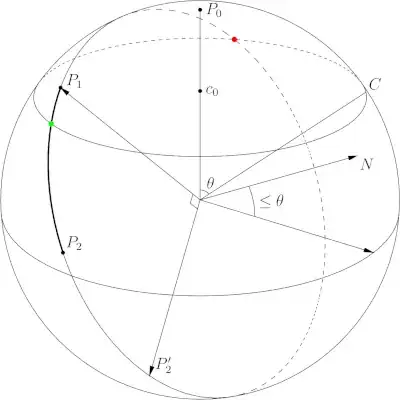
The edge of the circle is on a plane that cuts the sphere normal to the radius, call it the cplane.

The line segment is on a circle disk that passes through the two points on the sphere and passes through the origin. This circle is on a plane, call it the lplane.

The circle and line segment are on the sphere.

The strategy is to find the equations of the planes and solve them along with the sphere equation.

If real solutions exist then check that they are on the line segment.

Three points are required to determine the equation of a plane.

$$(R-R_0) \cdot N = 0 \tag{1}$$ $R = (x,y,z)$.$R_0$ is a fixed point on the plane. $N$ is the normal to the plane. Three points are required to find the normal.

cplane

The center point $(R,\theta_c,\phi_c)$ is not on the cplane.

---

Edit $1$ start:

The normal to the cplane is the vector from the origin $\mathbf{O}$ to the center of the circle, $N_c = (R,\theta_c,\phi_c)$.

$C_1 = \left(R,\theta_c +\frac{r}{R},\phi_c\right)$ and $C_2 = \left(R,\theta_c -\frac{r}{R},\phi_c\right)$ are two points on the circle radius $r$.

Convert $N_c$ and $C_1$ into Cartesian coordinates. Take $N_c$ and $R_0 = C_1$ plug them into $(1)$ this will give the equation of the cplane of the form:

Edit $1$ end:

---

$$ax + by + cz = d \tag{2}$$

lplane

The origin $\mathbf{O}$, $P_1$ and $P_2$ are three points that determine the lplane.

Convert $\mathbf{O}$,$P_1$ and $P_2$ into Cartesian coordinates.

Take $N_l = P_1 \times P_2$, $R_0 = \mathbf{O}$ plug them into $(1)$. This will give an equation of the form:

$$ex + fy + gz = 0 \tag{3}$$

The Sphere

$$x^2 + y^2 + z^2 = R^2 \tag{4}$$

Solution

Solve equations $(2),(3),(4)$. It forms a quadratic in one variable.

If the solutions are complex then there is no solution, (complex conjugates).

If there is one real solution or a real double root then the lplane touches the cplane on the sphere at one point.

If there are two real solutions then the lplane cuts the cplane on the sphere at two points.

The line segment $P_1P_2$ is only part of the lplane.

Are the solutions inside the line segment $P_1P_2$?

Take the path from $P_1$ to $P_2$ in the direction of $P_2-P_1$. There is the pathological case where they are $\pi$ degrees opposite each other.

It requires a parameterized equation of the path.

Let $\widehat{V}$ denote the unit vector in the direction of $V$.

Find the unit vector $\widehat{Q}$ in the lplane normal to $\widehat{P_1}$.

$\widehat{Q} = \widehat{(\widehat{P_2}-(\widehat{P_2} \cdot \widehat{P_1})\widehat{P_1})} \tag{5}$

The $P_1$ $P_2$ path can be parameterized as:

$$P = \widehat{P_1}R\cos(\alpha) + \widehat{Q}R\sin(\alpha) \tag{6}$$

At $\alpha_1 = 0$ then $P = \widehat{P_1}R = P_1$.

At $\alpha_2$ let $P_2 = \widehat{P_1}R\cos(\alpha_2) + \widehat{Q}R\sin(\alpha_2)$.

Solve for $\alpha_2$ in the positive sense $[0,2\pi)$.

At the solution $S(S_x,S_y,S_z)$

$$S = \widehat{P_1}R\cos(\alpha_s) + \widehat{Q}R\sin(\alpha_s) \tag{7}$$

Solve for $\alpha_s$ in the positive sense $[0,2\pi)$.

If $0 \le \alpha_s \le \alpha_2$ then the solution is on the line segment.

Is the line segment inside the circle?

There must be two real solutions for the line segment to be inside the circle.

Parameterize the circular arc starting from solution $1$ $S_1$ to solution $2$ $S_2$. Determine the angle of $S_2$ relative to $S_1$. Determine the angle of the points $P_1$ and $P_2$ wrt $S_1$. If the angles of $P_1$ and $P_2$ are less than the angle of $S_2$ then they are inside the curve. Note the arc from $S_1$ to $S_2$ is the same curve as from $P_1$ to $P_2$ but the angle starts at $S_1$. The direction from $S_1$ to $S_2$ is key.This method avoids complicated $2\pi - angle$ shortest angle scenarios that I could not resolve.

Let $\widehat{T}$ be normal to $\widehat{S_1}$ in the $\mathbf{O}S_1S_2$ plane.

$$\widehat{T} = \widehat{ \widehat{S_2} - (\widehat{S_2}\cdot \widehat{S_1}) \widehat{S_1} } \tag{8} $$

$$SPath = \widehat{S_1}R\cos(\beta) + \widehat{T} R \sin(\beta) \tag{9}$$

Solve $\beta$ for $S_2$,$P_1$ and $P_2$ on the SPath in a positive sense $[0,2\pi)$.

$$S_2 = \widehat{S_1}R\cos(\beta_{S2}) + \widehat{T} R\sin(\beta_{S2}) \tag{10}$$ $$P_1 = \widehat{S_1}R\cos(\beta_1) + \widehat{T} R\sin(\beta_1) \tag{11}$$ $$P_2 = \widehat{S_1}R\cos(\beta_2) + \widehat{T} R\sin(\beta_2) \tag{12}$$

If $0 \le \beta_1,\beta_2 \le \beta_{S2}$ then the line segment is inside the circle.