Update: Please also see this solution here provided by MattL.
I have the roots for a very large order polynomial (>100), and from those alone wish to recreate the polynomial and run into numerical challenges when using the poly function for doing this available in Matlab and Python (numpy).
I attempted to convolve the coefficients for the roots and still see numerical issues (although I am not sure why as the dynamic range of the interim results when convolving subsets of the roots is far below that allotted by the double precision floating point numbers I am using).
As a simple example, and showing where I begin to see issues: I start with a 59th order polynomial with unity coefficients: $1+x+x^2+\ldots x^{59}$
The roots of this will be the 60th roots of unity given as $e^{jn2\pi/60}$ with n from 1 to 59, which I also get from Python using np.roots which are then given as complex double precision floating point representation (real and imaginary are both double precision). I then used the roots to poly function within python and would expect to get the unity coefficients back, but instead get large errors in the middle of the polynomial (yes, consistent with where we would have the biggest sum of products).
I then used my own approach of iteratively convolving coefficients while watching for dynamic range issues. For example in the plot below, I first show the resulting polynomial if only the first half of the roots were used, with the magnitude in dB to show that the dynamic range is far below the 300 dB+ allotted by double precision floating point. The lower portion of this plot shows the result of convolving this polynomial returned by the first 30 roots with the similar polynomial returned by the second 30 roots with no improvement in error.
I went on to iteratively convolve each of the complex roots $z_n$, by convolving the first two (as $x-z_1$ and $x-z_2$), and then convolving the result of that with the next root (as $z^2-(z_1+z_2)+z_1 z_2$ and $x-z_3$), etc through all of the roots, as given in Python below:
def cz(roots):
z = list(roots)
result = [1]
while z:
result = np.convolve(roots, [1, -z.pop()])
return result
This resulted in even more error:
My question is two fold: what is the source of this numerical error and are their improved mathematical techniques that I could use for converting large numbers of roots (I would like to be able to extend this to 100s of roots) to its polynomial form? I used the roots of unity in this simple example, but more generally I would like to be able to do this with any arbitrary roots on the complex plane (and can limit it to roots that are on or inside the unit circle).
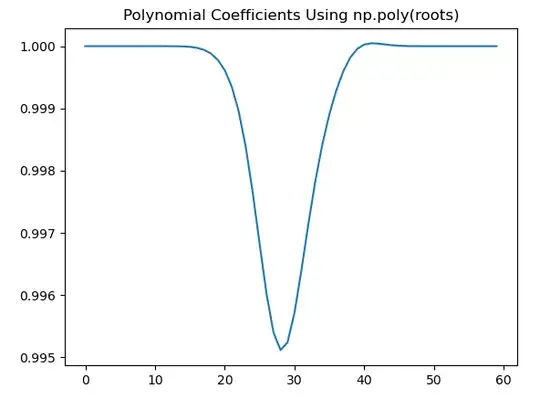

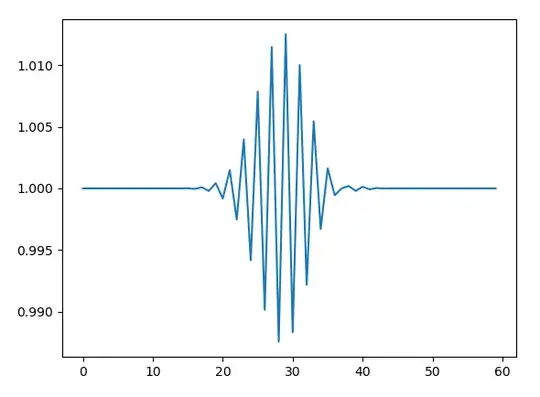
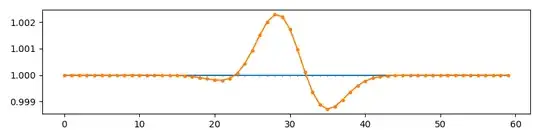
np.root(). I just confirmed now that what was returned, and what I could calculate directly using both of your approaches are all in agreement within the machine epsilon for floating point numbers (10E-15) – Dan Boschen Dec 04 '21 at 16:14