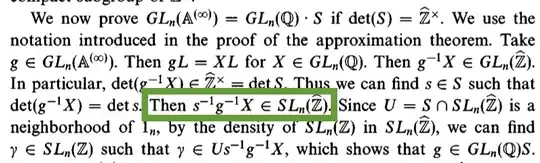I am stuck on some proofs concerning strong approximation in Chapter 3.1 of Hida's book on modular forms. I have put in green the things that I do not understand.
The set $gL\subset \mathbb{A}^\infty$ is a (free) module over $\widehat{\mathbb{Z}}$. But why can we assume that its basis vectors are in $\mathbb{Q}^n$? I think that it has something to do with the identity $\mathbb{A}^\infty=\mathbb{Q}+\widehat{\mathbb{Z}}$, but I do not see in what way?
We have $s,g\in GL_n(\mathbb{A}^\infty)$ and $X\in GL_n(\mathbb{Q})$ (why again? this has to do with the previous proof). Then $s^{-1}g^{-1}X$ surely is in $SL_n(\mathbb{A}^\infty)$, but why is it suddenly in $SL_n(\widehat{\mathbb{Z}})$?
Any help is much appreciated.