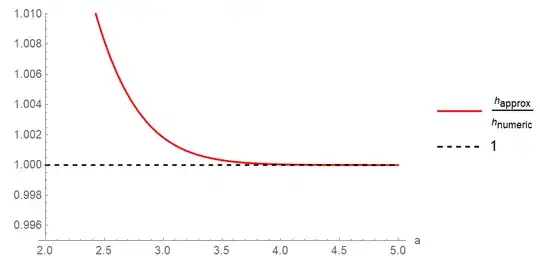
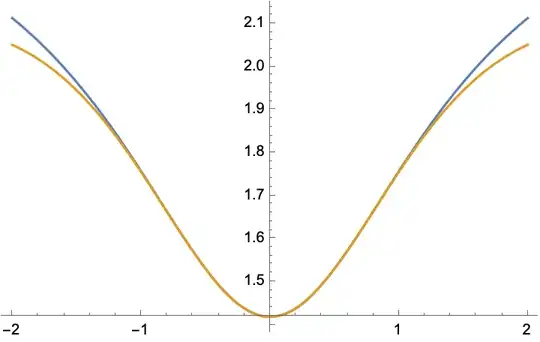
I've been trying to create a good approximation for this function:
$$h\left(a\right)\equiv-\int_{-\infty}^{\infty}p\left(x,a\right)\ln\left(p\left(x,a\right)\right)dx$$ where
$$p\left(x,a\right)\equiv\frac{1}{2\sqrt{2\pi}}\left(e^{-(x+a)^{2}/2}+e^{-(x-a)^{2}/2}\right)$$
This is just the entropy of a bimodal distribution, expanding in the distance of the modes from the center. I haven't been able to figure out the domain of convergence of the Taylor series, but it appears to be quite small:
$$h\left(a\right)=\frac{1+\ln\left(2\pi\right)}{2}+\frac{1}{2}a^{2}-\frac{1}{4}a^{4}+\frac{1}{6}a^{6}-\frac{5}{24}a^{8}+\frac{13}{30}a^{10}-\frac{227}{180}a^{12}+\frac{2957}{630}a^{14}\\-\frac{21425}{1008}a^{16}+\frac{642853}{5670}a^{18}+\ldots$$
I thought maybe a Pade approximation might be better than Taylor, but I always see those calculated from the Taylor Series, which won't work well here. So what can I do?
One thing I tried began with noting that $h(a)$ has a rather Gaussian shape, and so $\ln\left(\frac{h(\infty)-h(a)}{h(\infty)-h(0)}\right)$ is nearly a parabola. But the $a^2$ term of that expansion wasn't even a good fit to the parabola. But maybe a Padme approximation would fit this function better than it would to $h(a)$?
I'm really at a loss. There's something about this function that makes it difficult to even approximate well.