Hello I wok in the Brezis problem 5.31. It`s:
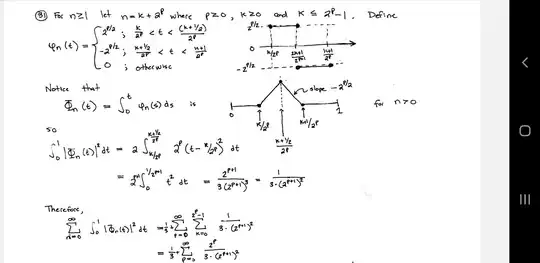
Given an integer $n\geq 1$ write $n = k + 2^{p}$ where $p,k\geq 0$ and $k \leq 2^{p}-1$. Define the function in $(0,1)$: $$\varphi_{n}(t)=\left\{ \begin{array}{ll} 2^{\frac{p}{2}} & \mbox{if $t \in \big(\frac{K}{2^p},\frac{K+\frac{1}{2}}{2^p}\big)$};\\ -2^{\frac{p}{2}} & \mbox{if $t \in \big(\frac{K+\frac{1}{2}}{2^n},\frac{K+1}{2^p}\big)$};\\ 0 &\mbox{otherwise} \end{array} \right. $$ Set $\varphi_{0} \equiv 1$ Prove that $(\varphi)_{n\geq}$ is an orthonormal of $L^{2}(0,1)$ basis.
In this thread it was proved that $(\varphi)_{n\geq}$ are orthonormal Let $\{ \psi_{j,k}(t)\}$ haar system. How to prove that it is orthogonal?. Now i want to prove that they are orthonormal basis. So i want to use the next result (Problem 5.30 Brezis):
Let $(e_{n})_{n \geq 1}$ be an orthonormal sequence in $L^{2}(0,1)$ if $$ \sum _{n=1}^{\infty}\int_{0}^{1}\left|\int_{0}^{t}p(s)e_{n}(s)ds\right| = \int_{0}^{t}|p(t)|^{2}(1-t)dt$$ and $p(t)\neq 0$ a.e, then $(e_{n})_{n\geq1}$ is an orthonormal basis.
So i want to prove that if: $$ \Phi_{n}(t)=\int_{0}^{t}\varphi_{n}(s)ds. $$ then $$ \sum _{n=1}^{\infty}\int_{0}^{1}\left|\Phi_{n}(t)\right|^{2} = \int_{0}^{t}(1-t)dt$$ But i don´t understand why: $$\int_{0}^{1}|\Phi_{n}(t)|^{2} = 2\int_{\frac{k}{2^{p}}}^{\frac{k+\frac{1}{2}}{2^{p}}}2^{p}\left (t-\frac{k}{2^{p}}\right)^{2}$$
Can someone help me?.