4

Could you please help by showing me how I can find the unknown sides for the triangles below?

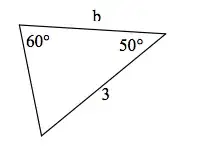
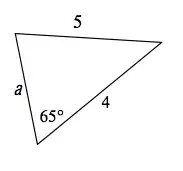
enter image description here

enter image description here

enter image description here

jaykirby
  • 850

2 Answers2

7

Hint: since you do not have a right triangle, and do not know whether the second triangle is a right triangle, assume it isn't:

For the first, use the law of sines: the unknown angle is $180 - 60 - 50 = 70^\circ$

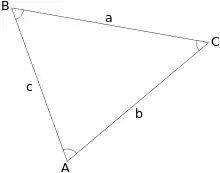
$$\frac a{\sin A} = \frac b{\sin B} = \frac c{\sin C}\tag{Law of Sines}$$

enter image description here

For the second triangle:

Use the law of cosines using the information you are given, to solve for the unknown, given the right choice of angles.

$$c^2 = a^2 + b^2 - 2ab\cos \gamma\tag{Law of Cosines}$$

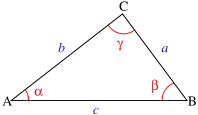
enter image description here

Images from the linked wikipedia articles (respectively).

amWhy
  • 210,739
  • Thanks, could you show me how you would apply the law of cosines to these examples? I'm confused with its application. – jaykirby Jun 26 '13 at 02:40
  • Ok, I think I follow. Would it be possible for you to solve the worked problem step by step so I can work backwards from there? I'm finding it hard to solve just by looking at the law of cosines.. – jaykirby Jun 26 '13 at 02:44
  • 3
    Try seeing what you can do...I'll be happy to help and guide you with the work you're doing, and step in once you show a little work. – amWhy Jun 26 '13 at 02:47
  • Ok thanks. I'm still trying to wrap my head around the sine rule and cosine rule. Apart from the formulas, maybe you could explain to me in simple terms how they work or what they mean? – jaykirby Jun 26 '13 at 02:48
  • 1
    The labels correspond to the images: match them up, and apply to your triangles: the unknown side will be the variable, everything else you'll have values for. E.g., in the law of sines, we know that $$\dfrac{b}{\sin 70}=\dfrac{3}{\sin 60} \iff {b} = 3 \cdot \dfrac{\sin 70}{\sin 60} \implies b\approx 3.255$$ Now, you give it a shot using the law of cosines for the second triangle. – amWhy Jun 26 '13 at 02:52
  • 1
    In using the law of cosines, set $c = 5$, $\gamma = 65^\circ$. Then you have $b = 4$, and $a$ the unknown variable to solve for. – amWhy Jun 26 '13 at 02:57
  • Makes sense, thanks. Just to clarify, how do you decide whether you should use sine rule or cosine rule? – jaykirby Jun 26 '13 at 03:12
  • 1
    Depends on the amount of information you have. In the first case, since you had the angles, and a side, you can easily solve the ratio of side/angle = unknown-sine/angle. When you have two sides and only one angle, there's no way of knowing the other two angles, so you use law of cosines, given two of the sides with one being a known side opposite a known angle, you can solve for the unknown side as the only unknown. – amWhy Jun 26 '13 at 03:15
  • So applying the cosine rule to the problem above: a2 = 25 + 16 -20xCos65? Is that right? – jaykirby Jun 26 '13 at 03:32
  • 1
    $c = 5$ and we express this with $c^2 = $, because the known angle is the angle opposite $c$. So, $c^2 = a^2 + b^2 -2a\cos(65) \iff 25 = a^2 + 16 -4a\cos(65)$. This gives us $a^2 - 4a\cos(65) = 25 - 16 = 9.$ So you have a quadratic equation, once you approximate $\cos 65$, with $a^2 - 4\cdot \cos(65)\cdot a - 9 = 0$. There will only be one valid will be two solutions, only one positive. – amWhy Jun 26 '13 at 03:36
  • isn't the cosine rule: a2=b2+c2-2bcCosA – jaykirby Jun 26 '13 at 03:42
  • Sure, answer accepted. Now I'm confused above solving the quadratic equation a2−4⋅cos(65)⋅a−9=0...is there an easier way to solve? – jaykirby Jun 26 '13 at 03:47
  • 1
    Comment about cosine rule: That would work if we had angle A, which would be the angle opposite side a, which we don't have. We have to work with what we have. We only know the angle opposite c, which is 65∘ – amWhy Jun 26 '13 at 03:51
  • Im kind of confused about applying the quadratic formula to this equation...could you please show me how you would do it? I know the quadratic formula but I'm having a complete brain fade today.. – jaykirby Jun 26 '13 at 03:57
  • 1
    $a = \dfrac{-(4)(.422) \pm \sqrt{16(.422)^2 + 36}}{2}$ One value will be negative, the other positive. You want the positive value, and that will be the length of side $a$. I get $a \approx 2.27,$ but try it yourself and see what you get. – amWhy Jun 26 '13 at 04:02
  • thanks amWhy, i got the same answer. – jaykirby Jun 26 '13 at 04:39
  • @amWhy,I uploaded another problem where both a side and an angle are unknown. Am I right in approaching it by first solving for the unknown angle using the sine rule...and then solving for the side Z using the cosine rule? – jaykirby Jun 26 '13 at 05:01
  • 1
    That would be a great way to proceed! Yes indeed. – amWhy Jun 26 '13 at 05:03
  • So Sinγ/6= sin40/2. Then, Sinγ=sin40/2 x 6. So, γ= inverse sign x sin40/2 x 6. Am I right there? – jaykirby Jun 26 '13 at 05:14
  • Thanks for letting me know, I've done it now. – jaykirby Jun 26 '13 at 05:47
  • 1
    Almost: we divide $\sin 40$ by the length of the side opposite that angle, which is $4$. $\dfrac {\sin γ}6 = \dfrac{\sin 40}{4}.$ so $\gamma = \sin^{-1}(\frac {6\sin 40}{4})$ – amWhy Jun 26 '13 at 05:47
  • yep, got that now. so the answer I get is 74.61 is that right? – jaykirby Jun 26 '13 at 05:49
  • 1
    Yup!! Now you can use the law of cosines to put, say, $4^2 = z^2 + 6^2 - 2\cdot 6\cdot z \cos(40)$. Again, we rearrange to get a quadratic equation in $x$ on the left hand side, with zero on the right hand side. Then, once again, we use the quadratic formula to solve for the "valid" value of z. – amWhy Jun 26 '13 at 05:58
  • Nice so z2+20-12zcos(40)=0 right? then apply quadratic formula? – jaykirby Jun 26 '13 at 06:08
  • 1
    Yup, you got it: but for the quadratic formula, it helps to arrange the quadratic from largest degree to smallest: $$z^2 - 12\cdot (\cos 40) z + 20 = 0$$ – amWhy Jun 26 '13 at 06:11
  • Gotcha. So z= 12 plus/minus square root of 144(cos40)squared minus 80 divided by 2? Not sure how to write properly with the symbols on here... – jaykirby Jun 26 '13 at 06:15
  • 1
    That's exactly right. – amWhy Jun 26 '13 at 06:17
  • Alright. so final step, this should be easy but I'm having one of those days. Should be 12 plus/minus 2.21 over 2? Wait doesn't that give me two answers then? – jaykirby Jun 26 '13 at 06:24
  • Yes I now have z=6±1.105. So from the above z= 4/sin(40)x sin(74.61)? – jaykirby Jun 26 '13 at 06:50
  • 1
    you should get $z = 6(\cos 40)\pm 1.105$. Try them both. Recall, since we determined the angle $\gamma $ or rather, in the picture, it's $\omega \approx 74.61$, we can now test which length for z works for the ratios (using the law of sines) satisfies $\frac z{\sin 74.61} \approx \frac 4{\sin(40)}$. It will be the greater root: $z = 6\cos(40) + 1.105$ – amWhy Jun 26 '13 at 06:50
  • 1
    The term $6$ in $z = 6\pm 1.105$ should be multiplied by a factor of $\cos 40$, see my comment above: recall, the coefficient of the middle term in the quadratic equation is given by $-12\cos 40$ – amWhy Jun 26 '13 at 06:53
  • Ok so why will it be the greater root? – jaykirby Jun 26 '13 at 06:58
  • 1
    Because it matches the value using the law of sines...the larger root, not the smaller root. Indeed, we could simply solve for $z$ based on the ratios from the law of sines, but it is always good to have the means to obtain the right value through either the law of sines or of cosines. – amWhy Jun 26 '13 at 07:01
  • @amWhy:Actually, solving z/sin74.61≈4/sin(40)..doesn't z=5.99? But 6cos(40)+1.105 =5.70 so am I missing something here? shouldn't the answers match.. – jaykirby Jun 26 '13 at 11:17
  • @amWhy or am I mistaken about that? – jaykirby Jun 27 '13 at 02:23
  • It might be a rounding error...for the angle: Since the first result (using the law of sines) is less likely to have errors (given how complicated the quadratic formula is), let's go with $z = 5.999...\approx 6$ – amWhy Jun 27 '13 at 02:32
  • Im confused now, you said earlier we can solve for z based on ratios for the law of sines...but doesn't sin74.61 relate to the side which is 6 in length rather than the unknown side z? – jaykirby Jun 27 '13 at 03:06
  • 1
    Ahhh, yes, I got mixed up a bit. Use the law of cosines value then $5.7...$ Otherwise, What we could do is take the angle we found first: $\omega = \gamma = 74.61,$ and add to that the other angle $40$ so that the angle opposite side $z = 180 - (40 + 74.61) = 65.39$, then use law of sines with the correct angle $\dfrac{z}{\sin(65.39)} = \dfrac{4}{\sin(40)}$ – amWhy Jun 27 '13 at 03:13
  • I thought something was amiss...in that case, z = 5.65 right? Also, I noticed that for the second problem, in applying the quadratic formula you wrote a= -4(.422) but shouldn't the minus infront of the 4 be cancelled out already because from the original equation there was already -4 and two negatives cancel to become a positive? – jaykirby Jun 27 '13 at 03:19
  • 1
    the minus sign may have been an oversight, I'm not remembering the quadratic equation. (i was up late yesterday working with math.se) So could have been. Yes, I think z = 5.65 works for us, with the corrected angle. – amWhy Jun 27 '13 at 03:34
  • No worries @amWhy appreciate your help! Just to clarify then with the second problem, the answer I'm getting after the quadratic formula is 3.96. Do you get same or am I missing something again? – jaykirby Jun 27 '13 at 03:38
  • Oh, I see what you're referring to...yes, that should be dahhh! Yes, the correct answer will be 3.96 (approx)! – amWhy Jun 27 '13 at 03:43
  • @amWhy is there another way to solve for problem two without using the quadratic formula? Can we solve it just by using the sine rule...first working out all the angles and then applying sine rule? – jaykirby Jun 27 '13 at 04:02
  • Yes, I think that could be done. You'd need another angle using Law of sines, then you'd have to subtract from 180 the two known angles, then you could solve for a. But we need to wrap up this thread...other users have "issues" with long comment threads! ;-) – amWhy Jun 27 '13 at 04:08
  • The best solution is to continue the conversation in chat. – Alexander Gruber Jun 27 '13 at 14:39
  • @amWhy: Wowww... a long story. +1 – Mikasa Jul 02 '13 at 09:17
3

For the first one, use the fact that the sum of the interior angles of a triangle is $180^o$ to find the $3$rd angle and then use the sine law.

The third angle is $180-50-60=70$

The sine law states that ratio of the sines of two angles of a triangle is equal to the ratio of their opposite side lengths.

We can use it to find $b$: $\dfrac{b}{3}=\dfrac{\sin70}{\sin60} \implies b\approx3.255$

For the second, use the cosine law using the formula provided by AmWhy. It's just the process of plugging in the values to yield the answer then.

Maazul
  • 2,516