For example:
The square root of 81 is 9.
Is this a proposition? I ask this because a proposition is where is it is meaningful to ask whether a statement is true or false but in this case it would always be true.
If it is a proposition, would it be a tautology, since 9 is the square root of 81?
In formal logic, a proposition is anything that's grammatically a statement (an expression that has or can have a truth value) as opposed to a term (an expression that refers to an object in the domain of discourse, like a number). So yes, $\sqrt{81}=9$ is certainly a proposition. The "actual" truth value of a statement has no bearing on whether it's a proposition.
The square root of $81$ is $9.$
In symbols: $$\sqrt{81}=9.$$ Yes, this is a statement, and it is clearly true (based on the conventional interpretation of the various symbols contained in the statement).
Notice that it contains no logical connective (and, or, conditional, negation, etc.); this means that it is an atomic statement; we might further symbolise this proposition as $P.$
a statement is true or false but in this case it would always be true. If it is a proposition, would it be a tautology
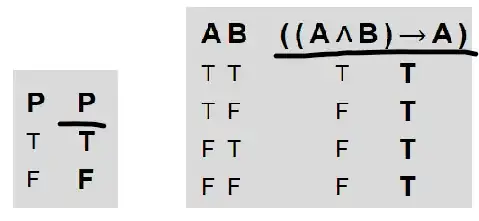
The truth table on the right shows that the compound statement $\;(A\land B)\to A\;$ is true regardless of what the atomic statements $A$ and $B$ stand for. In other words, $\;(A\land B)\to A$'s truth-functional form is always true. This means that $\;(A\land B)\to A\;$ is a tautology.
On the other hand, notice that if $P's$ meaning changes to "pigs can fly", or if we reinterpret the $\sqrt{\quad}$ symbol to output the negative root instead of the conventional positive root (so that $\sqrt{81}=9$ becomes false), then $P$ becomes a false statement (corresponding to the bottom row of $P$'s truth table). Since $P$'s truth table contains at least one 'false' entry, $P$ is patently not a tautology: its truth-functional form is not always true. In fact, no atomic statement can be a tautology.
In propositional logic, a tautology can also be understood as a proposition that is true regardless of its atomic propositions' assigned meanings.
Addendum to address the OP's follow-up questions
Your confusion stems from referring to $\sqrt{81}=9$ as “always true”, and conflating this with your impression that tautology means “always true”.
Firstly, ‘$\sqrt{81}=9$’ is not a propositional variable, just as ‘Pigs can fly’ isn't. However, both can be symbolised as the propositional variable $P.$
Secondly, please re-read the third-from-last and last paragraphs of my Answer above. Notice that asking whether a statement is a tautology involves inspecting its truth table, which requires the statement to first be symbolised in terms of propositional variable(s).
(Clearly then, a single propositional variable by itself cannot be a tautology.)
When considering whether $\sqrt{81}=9$ is a tautology, we are ignoring its particular guise, and considering just its abstract logical skeleton $P$ (as $P$'s assigned meaning varies).
The truth-functional form (logical skeleton $P$) of $\sqrt{81}=9$ is not always true; therefore, it is not a tautology. (In fact, $\sqrt{81}=9$ itself can be false, for example when working in base $12.)$ Calling $\sqrt{81}=9$ “always” true is not instructive; better to think of it as just “true”.
In contrast, $$1=1\to\big(1=1\:\lor\:2=3\big)$$ is a tautology.
Do you mean to ask whether tautologies are restricted to only compound propositions? Yes, they are.
Please don't overthink this. When in logic we talk about propositions, all we want to say is that it is something for which it makes sense to say that it is true or false.
Examples of propositions: Grass is green. Clark Kent is Superman. I have a billion rollers in my pocket. $\sqrt{81}=9$. $A\subseteq A$.
Examples of non-propositions: Can you open the window? Ouch!! Blubber. Ointment! $42$.
