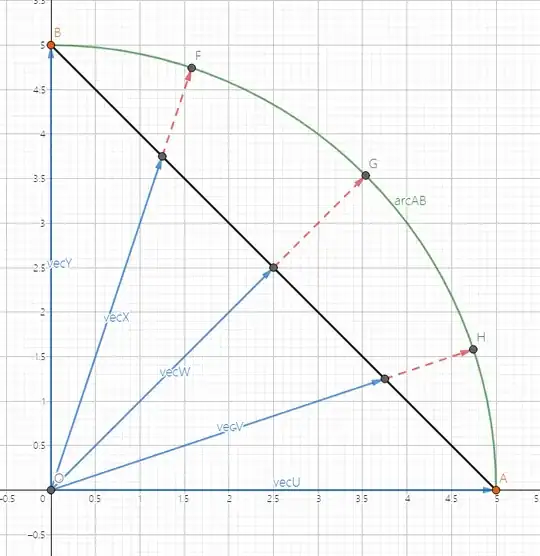
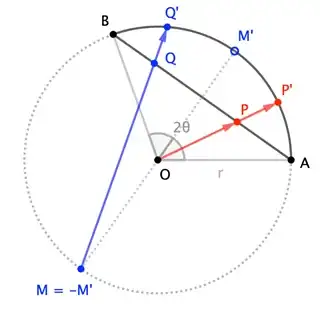
In $\bigcirc O$, let $\angle AOB=2\theta$. OP asks how to "push" chord $\overline{AB}$ to arc $\stackrel{\frown}{AB}$, and proposes specifically the strategy of projecting from the center $O$, as shown with points $P$ and $P'$ in these figures:
Formulating of the projection is simple: divide $\overrightarrow{OP}$ by its length, then scale it by the radius of the circle; ie,
$$\overrightarrow{OP'} = \frac{r}{|OP|} \overrightarrow{OP} \tag1$$
Less elegantly (but more-instructively), if we define $p := \dfrac{|AP|}{|PB|}$ (so that $P=\dfrac{A+pB}{1+p}$) as a parameter that ranges from $0$ (when $P=A$) to $\infty$ (when $P=B$), we can write
$$P' = \left(\;\frac{r (1 + p \cos2\theta)}{\sqrt{1 +
2 p \cos2\theta+p^2}}\;,\; \frac{r p\sin2\theta}{\sqrt{1+ 2 p \cos2 \theta+p^2}}\;\right) \tag2$$
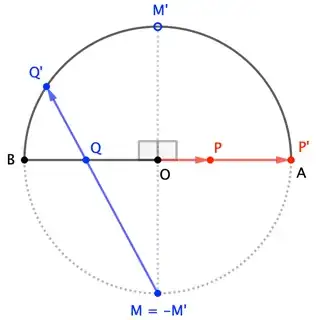
Unfortunately, such a projection is problematic when $\angle AOB=180^\circ$, as shown in the second figure; all the vectors $\overline{OP}$ are "flat", so their projections will only land at $A$ or $B$ (point $O$ projects to itself). This is reflected in how $(2)$ reduces when $\theta=90^\circ$:
$$P' = \left(\;\frac{r (1-p)}{|1-p|}\;,\; 0\;\right) \tag{2'}$$
In a comment, I suggested an alternative.
Instead of projecting from $O$, project from the midpoint of the "other" arc of the circle ($M$ in the figures), as shown with points $Q$ and $Q'$. Here, defining $q := \dfrac{|AQ|}{|AB|}$, we can write
$$Q' =\left(\;\frac{r (1 + 2 q \cos\theta + q^2 \cos2\theta)}{1 +
2q\cos\theta + q^2}, \frac{2r q \sin\theta(1 + q\cos\theta)}{1 +
2 q\cos\theta+q^2}\;\right) \tag3$$
This strategy works even when $\angle AOB = 180^\circ$, as the $\theta=90^\circ$ form of $(3)$ is
$$Q' =\left(\;\frac{r (1-q^2)}{1+q^2}, \frac{2rq}{1+q^2}\;\right) \tag{3'}$$
which, by interesting coincidence, corresponds to the Weierstrauss tangent-half-angle parameterization of the (upper semi)circle. (Fun Fact: It's not a coincidence!)
OP has commented that the second projection (via $M$) is "flawed" because it doesn't divide the arc evenly. This is true: except when $Q$ is the midpoint (or an endpoint) of the chord, the projection doesn't transfer the chord ratio to the arc; ie, $|AQ|:|QB|\neq|\stackrel{\frown}{AQ'}|:|\stackrel{\frown}{Q'B}|$. But this is also true of OP's projection (via $O$).
Indeed, there is no "geometric construction" (in the classical sense) to get from every $P$ on the chord to the corresponding $P'$ on the arc such that $|AP|:|PB|\neq|\stackrel{\frown}{AP'}|:|\stackrel{\frown}{P'B}|$. In particular, if $P$ "trisects" the chord then $P'$ would have to trisect the arc, giving a trisection of $\angle AOB$ which is a famously impossible thing to accomplish via straightedge-and-compass techniques. (So, it's certainly impossible to accomplish via a simple projection from some given point. See this answer for a quick proof when the point is the center of the circle.)
If $P'$ is required to divide the arc the same way $P$ divides the chord, for every $P$ on that chord, then essentially the best one can do is to write
$$P' = \left(r \cos\frac{2p\,\theta}{1+p}, r\sin\frac{2p\,\theta}{1+p}\right) \tag4$$
although this lacks the sense of geometrically "pushing" the chord to the arc.