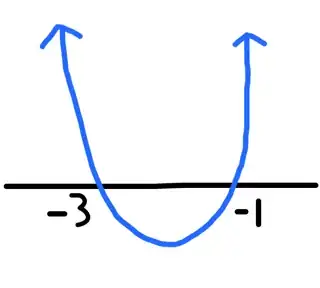
You have to consider several scenarios.
In general, when is $ab>0$? This happens when
- $a,b$ are both positive, or
- $a,b$ are both negative
So, consider: you have $(x+1)(x+3) > 0$. Then,
- $x+1,x+3$ are both positive, or
- $x+1,x+3$ are both negative
In your working, you assume only the former, and get that either $x > -1$ or $x>-3$. Of course, if both are positive, we need $x>-1$, so that gives one solution.
But what if both are negative? Then, when you solve $(x+1)(x+3) > 0$, you are dividing by one of those factors and therefore must reverse the inequality sign. Hence,
$$(x+1)(x+3) > 0 \implies x+1 < 0 \text{ or } x+3 < 0$$
when both are negative. Therefore, $x < -1$ or $x < -3$. Of course, again, we see that both factors are only negative if $x < -3$.
Thus, the solution set is the set of $x$ where $x > -1$ or $x<-3$.