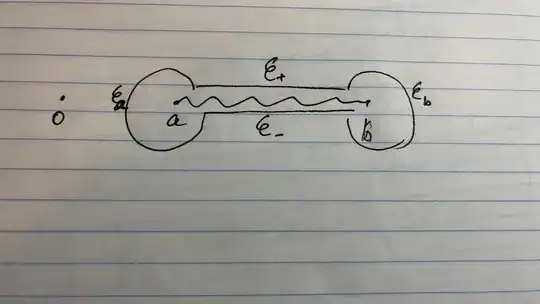
for the integral $\int_a^b \frac{\sqrt{(x-a)(b-x)}}{x} dx$, I am thinking use the contour
then since origin is not inside the contour, so we have $\int_{c-} + \int_{c_b} + \int_{c+} + \int_{c_a} \frac{\sqrt{(z-a)(b-z)}}{z} dz = 0$, but I dont know how to write out the integrals, is $I = \int_{c+} \frac{\sqrt{(z-a)(b-z)}}{z} dz$ and $\int_{c-} \frac{\sqrt{(z-a)(b-z)}}{z} dz = e^{i \pi} I$ ? and what about the two circle contour $\int_{c_b} +\int_{c_a} \frac{\sqrt{(z-a)(b-z)}}{z} dz $ thank you for any help