Derivative implies linear approximation

Question

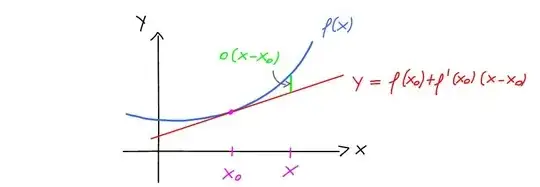
Consider $f: \mathbb R \to \mathbb R$ with the condition that $m = f'(x_0)$ exists. Show $f(x) \approx m(x - x_0) + f(x_0).$ If it looks like a weird exercise that nobody would ask, that's because I made it up. Please, see if the two proofs below work. Thanks.

Proof $1$. $$f'(x_0) = \lim_{x \to x_0}\frac{f(x) - f(x_0)}{x - x_0} \\ \iff \forall \epsilon > 0 \ \exists \delta \text{ s.t. } |x - x_0| < \delta \implies \left|\frac{f(x) - f(x_0)}{x - x_0} - f'(x_0)\right| < \epsilon $$

Since any real greater than $0$ is $\epsilon$ and absolute value is always nonnegative, we have that $|x - x_0| < \delta \implies \frac{f(x) - f(x_0)}{x - x_0} - f'(x_0) = 0$. But if we step out the $\delta$-neighborhood meaning $|x - x_0| > \delta$, we get $\frac{f(x) - f(x_0)}{x - x_0} - f'(x_0)\neq 0$. Thus for $x \approx x_0$ with $|x - x_0| < \delta$ or $|x - x_0| > \delta$, it follows $\frac{f(x) - f(x_0)}{x - x_0} - f'(x_0) \approx 0$.

Proof $2$.

Let $m$ be the slope of a tangent line $t$ to the straight line $l$. Let $s$ be the secant line to $l$ with the slope $k = \frac{f(x) - f(x_0)}{x - x_0}$. By definition, $s$ must intersect $l$ in at least two points. But if $s$ intersects $l$ in at least two places, $s$ must intersect $l$ everywhere. Also, $t$ coincides with $l$ everywhere. That means $m = k$.

Now let $q$ be a non-straight curve with $t$ tangent to $q$ at $x_0$ and $s$ intersecting $q$ in at least two places. As $x \to x_0, \ s$ approaches $t$. If $x$ gets so close to $x_0$ s.t. $x = x_0$, then we'd be dividing by $0$, so let $x \to x_0$ with $x \neq x_0.$ Then $s$ will never coincide with $t$. However, for $x$ extremely close to $x_0, \ s$ will also come extremely close to $t$ meaning we can make $|x - x_0|$ as small as we wish without having $x = x_0$ so that $m \approx k.$

Answer 1

You want to show that the function and the tangent line are very close to each other near the point of tangency.

Note that $$f'(x_0) = \lim_{x \to x_0}\frac{f(x) - f(x_0)}{x - x_0} \\ \iff \forall \epsilon > 0 \ \exists \delta \text{ s.t. } |x - x_0| < \delta \implies \left|\frac{f(x) - f(x_0)}{x - x_0} - f'(x_0)\right| < \epsilon\implies $$

$$\left| {f(x) - f(x_0)-f'(x_0)(x-x_0)}\right | < \epsilon |x-x_0|\implies $$

$$| f(x) - t(x) | < \epsilon |x-x_0|$$

Answer 2

We can proceed as follows

$$f'(x_0) = \lim_{x \to x_0}\frac{f(x) - f(x_0)}{x - x_0} \iff f(x)=f(x_0)+f'(x_0)(x-x_0)+o(x-x_0)$$

with $\frac{o(x-x_0)}{x-x_0} \to 0$ as $x \to x_0$, therefore when $x\approx x_0$ we can neclect the higher order term $o(x-x_0)$ to obtain

$$f(x)\approx f(x_0)+f'(x_0)(x-x_0)$$

which leads to the linear approximation (i.e. tangent line at $x=x_0$)

$$y= f(x_0)+f'(x_0)(x-x_0)$$