0

I was checking a Linkedin profile and I came across this statement in the “Grade” section. It’s a little confusing. It is as follows:

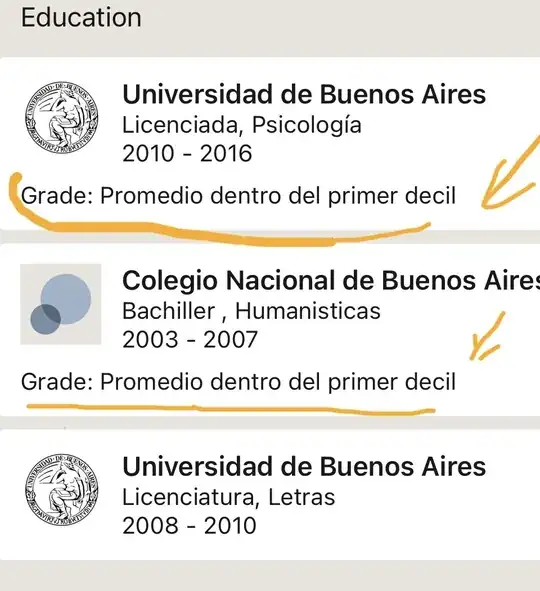
enter image description here

From the picture above, the statement in Spanish translates as: “Grade: gpa within the first decile”.

Is this statement correct? How’s interpreted?

Assuming that the GPA scale goes from 1 to 10 and not from 1 to 4, from the decile perspective we get the ordered set of grades:

1, 2,…, 10

Then, the first decile is: some value (x) is equal or smaller than the 10% or that the 90% is greater or equal than x. Taking this into account, wouldn’t we need a value in order to have the statement correct?

Example:

enter image description here

NaveganTeX
  • 111
  • It looks like 10% to me. When you googled "what is first decile", what came back? – John Douma Oct 03 '21 at 17:12
  • 1
    Usually in statistics the quantiles are numbered starting at the lowest scores. But in the Palo Alto data I see the deciles are numbered starting at the highest scores. Apparently to have a GPA in the top 10% of students at Gunn you need at least a $3.976.$ For LinkedIn profile we don't know exactly what GPA was required to be in the top 10% at those schools, but we are informed that this person was in the top 10% (unless "first decile" is for the lowest scores at those schools, which I doubt someone would put on their profile). – David K Oct 03 '21 at 17:25
  • 1
    The meaning of the "primer decil" seems simple enough. The person whose profile it is says their GPA was better than those of at least 90% of their classmates. It says nothing about what the GPA scale was at their schools. – David K Oct 03 '21 at 17:27
  • @DavidK Totally agree with you, David. The confusion came to me because of the mixing of the scales and the simplicity of that post. We would need further data to claim that their GPA is in the top 10%, since we do not know the scales. If you want to post your second answer, I approve right away! – NaveganTeX Oct 03 '21 at 17:36
  • @DavidK The first decile is the point that has 10% of the observations below it. And you’re saying that it has 10% of the observations above that point. This is because the deciles are numbered starting at the highest scores? – NaveganTeX Oct 03 '21 at 17:53

1 Answers1

1

The meaning of the notes in the LinkedIn profile seemed clear to me, but there are a number of ambiguities about the word decile to be aware of. These ambiguities also apply to the other kinds of quantile, such as quartile, quintile, and percentile.

First there is the question of which quantile is the "first" one in any set of data. Usually in descriptive statistics I expect to see the numbering of quartiles start near the bottom of the range of data and count up toward the top, so "first decile" normally would signify a data value that is less than the data values of any other decile. In class rankings, on the other hand, both in the Palo Alto schools and (I guess) in the schools attended by the LinkedIn member, students in the first decile have the highest GPAs in the entire school. This is exactly opposite from my experience with quantiles elsewhere.

Then there is the question of whether a particular "quantile" refers to a subset of the data or to a single data point that divides the subset into an upper group of data and a lower group of data. See the question "Are there $3$ or $4$ quartiles? $99$ or $100$ percentiles?" and its answers for more details. In the case of deciles, the question is whether there are $9$ of them or $10.$ If we consider a decile to be a single data point, for example one that lies between the lowest $10\%$ of the observed data and the highest $90\%,$ then there are $9$ deciles. 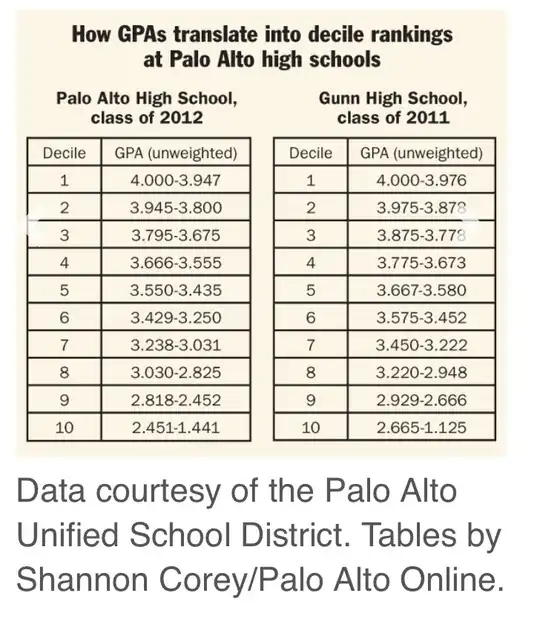In the Palo Alto schools, however, there are clearly $10$ deciles (we can see them numbered from $1$ to $10$ in the tables) and there are two GPA values listed for each decile, implying that a decile is not a single GPA value but encompasses a range of GPA values. For example, in the class of $2012$ in Palo Alto high school, any student with a GPA between $3.947$ and $4.000$ was in the first decile. This also implies that in that year, $10\%$ of students had GPAs in the range from $3.947$ to $4.000.$

I guess that in the schools in the LinkedIn profile, as in the schools in Palo Alto, "first decile" also means a high GPA, because who would put "first decile" on their profile if it meant you were near the bottom of your class? If that guess is correct, the owner of the LinkedIn has told us that their GPA was better than those of at least $90\%$ of their classmates at each of the first two schools listed in their LinkedIn profile.

They do not provide any data with which to support this claim; they give neither their own GPAs nor the minimum GPAs to be in the top decile in either school. But what should we expect? A photo of an official school transcript attached to a LinkedIn profile?

This is what a lot of descriptive statistics is about: summarizing information that is considered important (such as relative rank in a graduating class, in this case "in the top $10\%$") while omitting some details, such as the exact GPA of a particular person and the list of all GPAs of all students in the graduating class so you can confirm the "top decile" status. (Even the Palo Alto tables engage in some summarization: they fail to tell us how many students were in each decile or how many there were in total, and they fail to list the GPAs in each decile so that we can confirm that the boundaries were correctly set.)

By the way, a reason we might consider "first decile" to be more informative than a numeric GPA is that a numeric GPA is extremely sensitive to grade inflation, more so than a class rank. If the LinkedIn profile had listed "Gunn High School, class of 2011, GPA 3.870" without the table of deciles, would that have been as informative as "Gunn High School, class of 2011, third decile"? And if the profile had attached the table of deciles for Gunn High School class of 2011, forcing us to look up the decile ourselves, would the additional data have added much actual information?

David K
  • 108,155