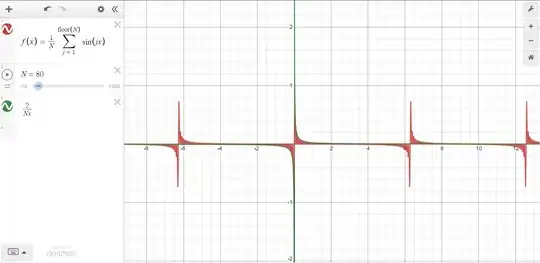
I've come across this beautiful expression, I would like to share how nicely the function $\displaystyle\frac{1}{N}\displaystyle\sum_{j=1}^{N}{\sin(jx)}$ fits into $\displaystyle\frac{2}{Nx}$, for all x in ($-2\pi,2\pi$). But how can I prove it? I tried taking the derivative of the function to get its maximum value but got nowhere. I'm still a student who hasn't yet formally encountered the topics I may need to reach the solution: Since this place is full of experts I thought it was a good idea to post this problem here. Thanks in advance for your time.
-
3Maybe you would be interested in the relation $\sin(jx) = \text{Im}(\exp(ijx))$, which leads to a geometric sequence. – Átila Correia Sep 29 '21 at 20:33
-
Something similar to this. – rtybase Sep 29 '21 at 20:40
-
1Or this. – rtybase Sep 29 '21 at 20:54
1 Answers
Getting the sum is a fun exercise in algebra. Using $\sin(kx) = \operatorname{Im}(e^{ikx})$
$$\sum_{k=1}^Ne^{ikx} = \frac{e^{i(N+1)x}-e^{ix}}{e^{ix}-1} = e^{i\left(N+1\right)\frac{x}{2}}\frac{\sin\left(N\frac{x}{2}\right)}{\sin\left(\frac{x}{2}\right)}$$
$$\implies \frac{1}{N}\sum_{k=1}^N\sin(kx) = \frac{\sin\left(N\frac{x}{2}\right)\sin\left((N+1)\frac{x}{2}\right)}{N\sin\left(\frac{x}{2}\right)}$$
Now an oscillatory envelope $f$ will always look like $f(x)g(x)$ where $g$ contains all of the oscillatory behavior so that the following holds
$$-|f| \leq f\cdot g \leq |f|$$
In this case the "non-oscillatory" part is the more slowly varying sine:
$$-\frac{1}{N}\csc\left(\frac{x}{2}\right)\leq\frac{\sin\left(N\frac{x}{2}\right)\sin\left((N+1)\frac{x}{2}\right)}{N\sin\left(\frac{x}{2}\right)}\leq \frac{1}{N}\csc\left(\frac{x}{2}\right)$$
for $x\in(-\pi,\pi)$, which is the actual function you are seeing. It relates to $\frac{2}{Nx}$ by small angle approximation.
- 37,891