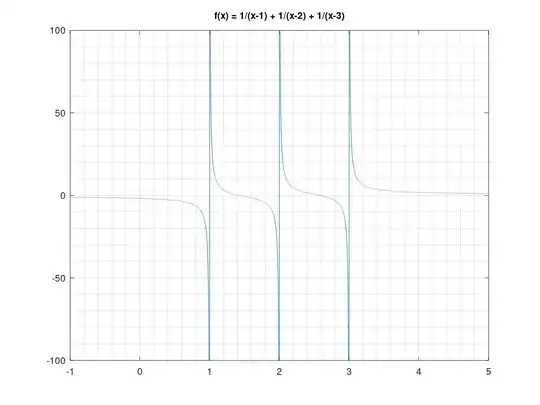
I am trying to solve for $x$ s.t. $$\sum_i^n \frac{1}{x-a_i}=0$$
or
$$\sum_i^n \frac{1}{x-a_i}\rightarrow0$$
$a_i$ is an arbitrary real number. A trivial solution is $x \rightarrow \infty$, and sometimes there aren't other solutions. But when there are nontrivial solutions, how would we be able to solve/approximate them numerically?
I am interested in a case where $n$ is very large so it is impractical to write down an analytic expression of $x$.
EDIT: This is a response to a commenter who asked to provide context. This question comes from a research problem that I am working on. Say I have a symmetric positive definite matrix $M=QAQ^T$ where $A$ is a real diagonal matrix and $Q$ is an orthonormal matrix. I want to find $\lambda$ that satisfies:
$$\left(M-\lambda I \right)^{-1}_k z =0$$
where $\left(M-\lambda I \right)^{-1}_i$ means a $k^{th}$ row of $\left(M-\lambda I \right)^{-1}$. This equality constraint is only applied to one row, which in this case is $k^{th}$ row, and all other rows do not have any constraint.
$$\left(M-\lambda I \right)^{-1} = Q(A-\lambda I)^{-1}Q^T z = Q(A-\lambda I)^{-1}b$$
where $b=Q^T z$. In other words, we want to solve
$$ Q_k(A-\lambda I)^{-1}b = 0$$
where $Q_k$ is $k^{th}$ row of $Q$. Now this has the following form:
$$\sum_i^n \frac{c_i}{a_i-\lambda}=0$$
I figured it will be sufficient to ask a simpler question: how to solve for $x$ such that
$$\sum_i^n \frac{1}{x-a_i}=0$$