As in this previous post, conic section homogenization is used to find the pair of straight lines joining the points of intersection of a specific line with the conic.
In several cases, though, it becomes apparent that the expected pair of straight lines isn't always the obtained solution. For example, I tried homogenizing a line with itself (squaring its own equation to use it as a degenerate conic of the general form) and got $0=0$, which is the equation of the whole plane. Apart from the obvious explanation, this makes sense, since every conceivable line that passes through the origin - which makes up the whole plane - can be reasoned to be a solution to the resulting homogenized equation.
For another example, I tried homogenizing a hyperbola with a line of the same slope as its asymptote to get, and besides the expected line, the original asymptote too;
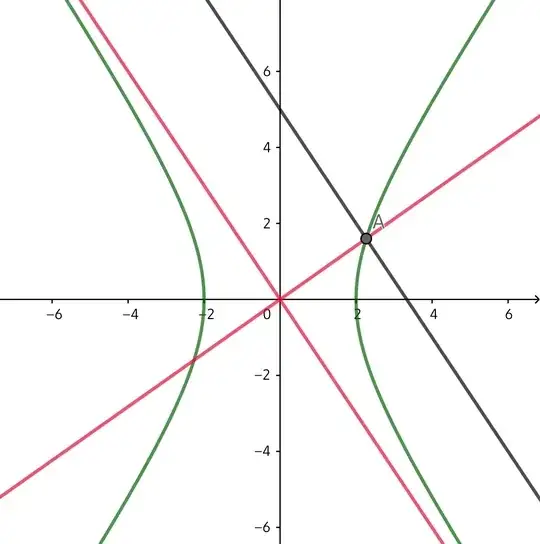
This doesn't make sense in a Euclidean geometry setting, so it was totally unexpected.
Considering such cases, I'd like to evaluate what results homogenization generally gives, but to derive it algebraically would be really cumbersome. Could someone point out an easier way to do this? For non-degenerate conics, the only cases where this sort of thing can happen seem to be when you do it with either tangents, similar lines as above for hyperbolas, and the axis of a parabola.