I've been doing some recreational maths on the Calkin–Wilf tree, which enumerates all positive irreducible fractions in the form of a binary tree, similar to the Stern–Brocot tree. Instead of enumerating all positive rational numbers, I became interested in finding a tree that generates only a particular subset of rationals, namely those of the form $m/n$ with the properties:
- $m/n$ is positive and irreducible,
- $m > n$,
- $m$ and $n$ have opposite parity.
You may already know where I'm going with this. After some trial-and-error, I indeed managed to find a set of transformations that accomplish this; in fact, I found two sets of transformations. The first set looks like this:
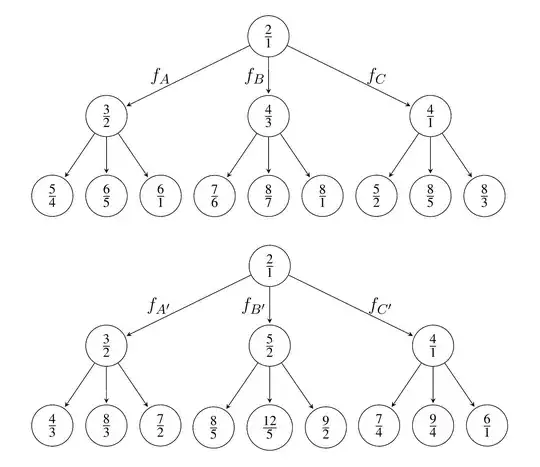
$$ f_A\left(\frac{m}{n}\right) = \frac{m+n}{2n},\qquad f_B\left(\frac{m}{n}\right) = \frac{2m}{m+n},\qquad f_C\left(\frac{m}{n}\right) = \frac{2m}{m-n}, $$
or in matrix form:
$$ \begin{pmatrix} m_A\\ n_A \end{pmatrix} = \begin{pmatrix} 1 & 1\\ 0 & 2 \end{pmatrix} \begin{pmatrix} m\\ n \end{pmatrix},\quad % \begin{pmatrix} m_B\\ n_B \end{pmatrix} = \begin{pmatrix} 2 & 0\\ 1 & 1 \end{pmatrix} \begin{pmatrix} m\\ n \end{pmatrix},\quad % \begin{pmatrix} m_C\\ n_C \end{pmatrix} = \begin{pmatrix} 2 & 0\\ 1 & -1 \end{pmatrix} \begin{pmatrix} m\\ n \end{pmatrix}. $$
The second set of transformations is $$ f_{A'}\left(\frac{m}{n}\right) = \frac{2m-n}{m},\qquad f_{B'}\left(\frac{m}{n}\right) = \frac{2m+n}{m},\qquad f_{C'}\left(\frac{m}{n}\right) = \frac{m+2n}{n}, $$ or $$ \begin{pmatrix} m_{A'}\\ n_{A'} \end{pmatrix} = \begin{pmatrix} 2 & -1\\ 1 & 0 \end{pmatrix} \begin{pmatrix} m\\ n \end{pmatrix},\quad % \begin{pmatrix} m_{B'}\\ n_{B'} \end{pmatrix} = \begin{pmatrix} 2 & 1\\ 1 & 0 \end{pmatrix} \begin{pmatrix} m\\ n \end{pmatrix},\quad % \begin{pmatrix} m_{C'}\\ n_{C'} \end{pmatrix} = \begin{pmatrix} 1 & 2\\ 0 & 1 \end{pmatrix} \begin{pmatrix} m\\ n \end{pmatrix}. $$ Starting with $2/1$, we obtain the two trees
It is straightforward to prove that each tree indeed enumerates all rationals with the properties 1-3, without duplicates (I'll leave that as an exercise).
Unlike the binary Calkin–Wilf and Stern–Brocot trees, these trees are ternary. My question is: is there a deeper reason for this? Why do these transformations come in sets of three? Can it be proven that these two are the only possible sets of transformations?
If you are wondering why I'm interested in these fractions, there is a fascinating link between the trees I found and the two known trees of Pythagorean triples. Indeed, the tuples $(m,n)$ with the properties 1-3 generate all primitive Pythagorean triples as $(m^2-n^2, 2mn, m^2+n^2)$. You can check that
$$ \begin{align} \begin{pmatrix} 2 & 1 & -1\\ -2 & 2 & 2\\ -2 & 1 & 3 \end{pmatrix} \begin{pmatrix} m^2 - n^2\\ 2mn\\ m^2 + n^2 \end{pmatrix} &= \begin{pmatrix} m_A^2 - n_A^2\\ 2m_A\,n_A\\ m_A^2 + n_A^2 \end{pmatrix},\\[1em] % \begin{pmatrix} 2 & -1 & 1\\ 2 & 2 & 2\\ 2 & 1 & 3 \end{pmatrix} \begin{pmatrix} m^2 - n^2\\ 2mn\\ m^2 + n^2 \end{pmatrix} &= \begin{pmatrix} m_B^2 - n_B^2\\ 2m_B\,n_B\\ m_B^2 + n_B^2 \end{pmatrix},\\[1em] % \begin{pmatrix} 2 & 1 & 1\\ 2 & -2 & 2\\ 2 & -1 & 3 \end{pmatrix} \begin{pmatrix} m^2 - n^2\\ 2mn\\ m^2 + n^2 \end{pmatrix} &= \begin{pmatrix} m_C^2 - n_C^2\\ 2m_C\,n_C\\ m_C^2 + n_C^2 \end{pmatrix}, \end{align} $$ and $$ \begin{align} \begin{pmatrix} 1 & -2 & 2\\ 2 & -1 & 2\\ 2 & -2 & 3 \end{pmatrix} \begin{pmatrix} m^2 - n^2\\ 2mn\\ m^2 + n^2 \end{pmatrix} &= \begin{pmatrix} m_{A'}^2 - n_{A'}^2\\ 2m_{A'}\,n_{A'}\\ m_{A'}^2 + n_{A'}^2 \end{pmatrix},\\[1em] % \begin{pmatrix} 1 & 2 & 2\\ 2 & 1 & 2\\ 2 & 2 & 3 \end{pmatrix} \begin{pmatrix} m^2 - n^2\\ 2mn\\ m^2 + n^2 \end{pmatrix} &= \begin{pmatrix} m_{B'}^2 - n_{B'}^2\\ 2m_{B'}\,n_{B'}\\ m_{B'}^2 + n_{B'}^2 \end{pmatrix},\\[1em] % \begin{pmatrix} -1 & 2 & 2\\ -2 & 1 & 2\\ -2 & 2 & 3 \end{pmatrix} \begin{pmatrix} m^2 - n^2\\ 2mn\\ m^2 + n^2 \end{pmatrix} &= \begin{pmatrix} m_{C'}^2 - n_{C'}^2\\ 2m_{C'}\,n_{C'}\\ m_{C'}^2 + n_{C'}^2 \end{pmatrix}. \end{align} $$ The first set of 3x3 matrices was discovered by Price (2008), the second by Berggren (1934) and Barning (1963) (see the wiki article). At the time I was unaware of these matrices, so I was surprised to find out that I re-discovered something that wasn't known until fairly recently, with just a few days of mathematical doodling...
I've done some reading on these trees, including this top answer on 'near-Pythagorean' triplets, but I'm wondering if my own questions can be answered without any reference to Pythagorean triplets.