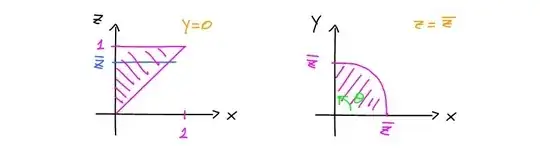
Compute $\int_{0}^{1}\int_{0}^{z}\int_{0}^{\sqrt{z^2-x^2}} \dfrac{e^{z^2}}{\sqrt{x^2+y^2}}\, dy\, dx\, dz$ using this change of coorninates.

Question

Compute $\int_{0}^{1}\int_{0}^{z}\int_{0}^{\sqrt{z^2-x^2}} \dfrac{e^{z^2}}{\sqrt{x^2+y^2}}\, dy\, dx\, dz$ using this change of coorninates.

I could say that: $0\leq 1, 0\leq x\leq z, 0\leq y \leq \sqrt{z^2-x^2}$

I believe that cylindrical and not spherical coordinates should be used. But the calculation has become difficult for me, I think there are more things to consider.

If $x=r\cos\theta, y=r\sinθ, z=z$, then

$$\int_{0}^{1}\int_{0}^{z}\int_{0}^{\sqrt{z^2-r^2\cos \theta}} e^{z^2}\, dr\, d\theta\, dz$$

The limit of integration $\sqrt{z^2-r^2\cos \theta}$ stays like this, or I must do something else.

Answer 1

For the given domain of integration, according to the following sketch

by cylindrical coordinates, which is indeed a good idea, we obtain

$$\int_{0}^{1}\int_{0}^{z}\int_{0}^{\frac \pi 2} e^{z^2}\, d\theta\, dr\, dz=\frac \pi 2\int_{0}^{1} ze^{z^2}dz$$