The root system $(V,\Delta)$ of type $A$ is usually defined as a subset of $\mathbb{R}^{n+1}$: $$ \{ e_i - e_j ;\, 1 \leq i,j \leq n+1,\, i \neq j\}. $$ However these vectors span an $n$-dimensional vector space, meaning that $V$ is isomorphic (as a vector space) to $\mathbb{R}^n$. Can anybody point me to a definition of the root system given directly in terms of $\mathbb{R}^n$? That is, not in terms of an embedding of $V$ into $\mathbb{R}^{n+1}$.
-
3Consider that all these vectors are orthogonal to the vector $(1,\dots,1)=\sum_ie_i$, so orthogonally project everything to the hyperplane $(1,\dots,1)^\perp$. – David Sheard Sep 04 '21 at 22:11
-
@DavidSheard: I actually don't understand your comment. As you say, all those vectors already are in the hyperplane $(1,...,1)^{\perp}$, so when one orthogonally projects them to that hyperplane ... nothing happens, right? So that presumably does not answer OP's question. What am I overlooking? – Torsten Schoeneberg Sep 06 '21 at 04:27
-
@TorstenSchoeneberg you are right I did not phrase it very well at all. I should have said: turn ${e_1-e_2,...,e_n-e_{n-1}}$, into an orthonormal basis of $(1,\dots,1)^\perp$, then write everything in this basis. I think the result will be a mess, not having the symmetry of the original representation of the root system. To be concrete, consider the root system of $A_2$ in $\mathbb{R}^3$. In $(1,1,1)^\perp$, it's the vertices of an equilateral triangle which wont look good in the standard basis of $\mathbb{R}^2$. – David Sheard Sep 06 '21 at 09:27
-
@DavidSheard: I see, but I think you don't mean to "turn" those $e_i-e_{i+1}$ into an orthonormal basis, rather to express them in terms of an orthonormal basis. That's what I do in my answer now, and of course it confirms what you say, the result is kind of a mess, and the vertices do not look good when written in the standard basis. – Torsten Schoeneberg Sep 07 '21 at 20:06
-
1@TorstenSchoeneberg By turn I meant use them as input for the Gram-Schmidt algorithm, which I think is a fair use of the verb. Anyway, I admire your determination in working out all the details! – David Sheard Sep 07 '21 at 21:16
1 Answers
What is a root system? It's a bunch of vectors with high symmetry between them. How do we phrase it mathematically? We imagine these vectors in some Euclidean space and talk about lengths and angles. What is the mathematical encoding of lengths and angles? It's a scalar product, and we need one such that all the "symmetries" of the root system preserve this scalar product.
In most definitions, a root system $R$ does not qua definition come with a scalar product $\langle \cdot, \cdot\rangle$ invariant under its Weyl group; however, any definition implictly gives us such a scalar product i.e. notions of lengths and angles (it is implicit in the definition of either the reflections $s_\alpha$, which we want to imagine as reflections with respect to hyperplanes orthogonal to $\alpha$; or in the definitions of the coroots $\check\alpha$, which we want to imagine as measuring the length of the orthogonal projection onto the line through $\alpha$).
The root system $A_n$ has a basis (both in the sense of root system basis, and basis of the ambient vector space) $\alpha_1, ..., \alpha_n$ whose geometry (angles and lengths) can be completely described by the relations
$$\langle \alpha_i, \alpha_j \rangle = \begin{cases} 2 \text{ if } i=j\\-1 \text { if } i=j \pm 1 \\ 0 \text{ else} \end{cases}$$
(and the whole root system consists of all $\pm (\alpha_i + \alpha_{i+1}+...+\alpha_j$) for $i\le j$).
Now when you say you would like to describe that as a subset of $\mathbb R^n$, you can either
- just choose any basis $v_1, ..., v_n$ of $\mathbb R^n$ and declare a new scalar product $\langle \cdot,\cdot \rangle_{new}$ on this $\mathbb R^n$ via $$\langle v_i, v_j \rangle_{new} = \begin{cases} 2 \text{ if } i=j\\-1 \text { if } i=j \pm 1 \\ 0 \text{ else.} \end{cases}$$
There you have embedded the root system into an Euclidean space, but with a funny scalar product which does not match our intuition of Euclidean lengths and angles. The fact that this is so easy shows that it is not very helpful.
Rather, what this should mean is that you want to
- use $\mathbb R^n$ with its standard scalar product $\langle \cdot,\cdot \rangle_{st}$, i.e. declare the standard basis $e_1 := (1,0,...,0), ..., e_n:=(0,...0,1)$ to be an orthonormal basis, and then "realize" the root system in there. That is, find a specific set of $n$ linearly independent vectors $\beta_1, ..., \beta_n$ inside this Euclidean space $(\mathbb R^n, \langle \cdot,\cdot \rangle_{st})$ such that $$\langle \beta_i, \beta_j \rangle_{st} = \begin{cases} 2 \text{ if } i=j\\-1 \text { if } i=j \pm 1 \\ 0 \text{ else.} \end{cases}$$
So now, of course, most bases will not work as $\beta_1, ..., \beta_n$. But surely we can always find such bases. We can even do it in such a way that we have kind of canonical inclusions $A_n \subset A_{n+1}$ along the inclusions $\mathbb R^{n} \subset \mathbb R^{n+1}$. Indeed, obviously for $n=1$ we have to take one of
$\beta_1 = \pm \sqrt 2 e_1$.
(and get the same root system regardless of the sign we choose). For $n=2$ a quick calculation shows that if we set $\beta_1 = \sqrt 2 e_1 = (\sqrt2,0)$, then we have to pick one of
$\beta_2 = -\sqrt{\frac12} e_1 \pm \sqrt{\frac32}e_2 = (-\sqrt{\frac12}, \pm\sqrt{\frac32})$.
For $n=3$, if we choose $\beta_1 = (\sqrt2,0,0), \beta_2=(-\sqrt{\frac12}, \sqrt{\frac32},0)$, then we need $\beta_3$ to be one of
$-\sqrt{\frac23} e_2 \pm\sqrt{\frac43}e_3 = (0,-\sqrt{\frac23},\sqrt{\frac43})$.
At this point, it should be obvious there's a pattern, and indeed we can "realize" the root system $A_n$ within the Euclidean space $\mathbb R^n, \langle \cdot ,\cdot \rangle_{st})$ via choosing as basis roots:
$$\boxed{\beta_1 := \sqrt2 e_1 = (\sqrt 2, 0, ..., 0, 0), \\ \beta_2 := -\sqrt{\frac12} e_1 + \sqrt{\frac32}e_2 = (-\sqrt{\frac12}, \sqrt{\frac32},0,...,0)\\ \beta_3 :=-\sqrt{\frac23} e_2 +\sqrt{\frac43}e_3 = (0,-\sqrt{\frac23},\sqrt{\frac43},0,...,0) \\ \vdots \\ \beta_n := -\sqrt{\frac{n-1}{n}} e_{n-1}+\sqrt{\frac{n+1}{n}}e_n = (0,..., 0, -\sqrt{\frac{n-1}{n}}, \sqrt{\frac{n+1}{n}})}$$
So there you have it. Compare my related answer to Picture of Root System of $\mathfrak{sl}_{3}(\mathbb{C})$. Note that in this standard image of $A_2$
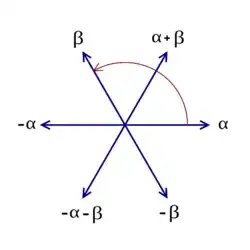 the lengths are not given, and of course one can scale either the vectors or the scalar product so that the roots have length $1$ (instead of $\sqrt 2$), and then imagine $\beta_1 = (1,0)$ (called $\alpha$ in the picture), and $\beta_2 = (-\frac12, \frac12 \sqrt3)$ (called $\beta$ in the picture). But notice that for any $n\ge 2$, no scaling will remove all the roots from the coefficients!
the lengths are not given, and of course one can scale either the vectors or the scalar product so that the roots have length $1$ (instead of $\sqrt 2$), and then imagine $\beta_1 = (1,0)$ (called $\alpha$ in the picture), and $\beta_2 = (-\frac12, \frac12 \sqrt3)$ (called $\beta$ in the picture). But notice that for any $n\ge 2$, no scaling will remove all the roots from the coefficients!
You will now see how much more convenient that presentation in the $n$-dimensional subspace $\{(a_1, ..., a_{n+1}) \in \mathbb R^{n+1} : \sum a_i =0 \}$, with the scalar product being the restriction of the standard scalar product from $\mathbb R^{n+1}$, is: Where you can just identify the $\alpha_i$ with $\gamma_i := e_i-e_{i+1} = (0,...,0,1,-1,0,...,0)$, get all nice integer coefficients, and see a lot of this root system's symmetry -- that symmetry is hidden by those nasty root coefficients if you try to press the thing into the standard $\mathbb R^n$! Indeed, from looking at the vectors in the box alone, would you have guessed that flipping $\beta_i \mapsto \beta_{n-i}$ defines an isometric automorphism of the root system?
Also, there is a deeper reason for that identification with a subspace of $\mathbb R^{n+1}$. (This is related to parts of my answer to Basic question regarding roots from a Lie algebra in $\mathbb{R}^2$)
Namely, something happens on the way to get $A_n$ as the root system of e.g. the Cartan subalgebra of diagonal matrices in the Lie algebra $\mathfrak{sl}_{n+1}$. There, the space of diagonal matrices of $\mathfrak{gl}_{n+1}$ has dimension $n+1$, and so does its weight space; but when we restrict to the trace $0$ subspace, we lose one dimension, and the weight space spanned by the roots has only $n$ dimensions. An obvious standard basis of the weights on the diagonal matrices in $\mathfrak{gl}_{n+1}$ just consists of those that pick out one of the diagonal entries; there are $n+1$ of them. But when we restrict to those matrices with trace zero, we lose one dimension; and a good basis now are the ones which take the difference of the first and second, second and third, ..., $n$-th and $n+1$-th entry. More strikingly this is visible on the coroots: The diagonal matrices in $\mathfrak{gl}_{n+1}$ have basis
$$diag(1,0,...,0), diag(0,1,0,...,0), ..., diag(0,...,0,1)$$
but those in $\mathfrak{sl}_{n+1}$ have as a good basis
$$diag(1,-1,0,...0), diag(0,1,-1,0,...,0), ..., diag(0,...,0,1,-1)$$
and these are exactly the coroots to $\alpha_1, ..., \alpha_n$ in the root system $A_n$ (which happens to be self-dual, so these can even be naturally identified with the roots).
- 29,325