An Intriguing Question on Hyperbola!

Question

Let tangents $PA$ and $PB$ on hyperbola from any point $P$ on the Director Circle of hyperbola such that $d(P,AB).d(C,AB)=4d(S_1,PA).d(S_2,PA)$ and $|AS_1-AS_2|=4$ where $d(P,AB)$ denotes distance of point $P$ to the line $AB$ and $S_1$ and $S_2$ are the foci and $C$ is centre of the hyperbola. If asymptotes of hyperbola pass through the point $(1,2)$ and a line $y=4$ intersects the branch of hyperbola which lies entirely on the first quadrant only at a point then find the length of traverse axis of the hyperbola and its equation.

This is originally a question i had encountered in a test I had given, and i do know however that the director circle is the circle from which a pair of perpendicular tangents can be drawn and from the question it becomes clear that $2a=4$ but I am unable to make any use of the equation $d(P,AB).d(C,AB)=4d(S_1,PA).d(S_2,PA)$ maybe it is some property of hyperbola I am unaware of, in the given 'solution' they had directly stated the value of $b$ (of hyperbola) but I have no idea how they got that and I would highly appreciate any help with this question as it had been bugging me for quite a while now, thanks!

Answer 1

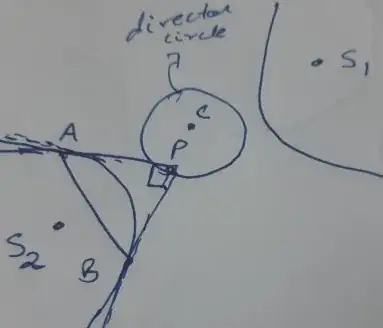
It is not a horizontal or vertical hyperbola - it has one branch which is entirely in the first quadrant and with other information provided, this fact will become clear as we go through the solution steps.

There are properties of hyperbola that would hold regardless of whether you rotated or shifted the coordinate axes. So let's work through them, first considering a hyperbola in a coordinate system such that,

$\displaystyle \frac{X^2}{a^2} - \frac{Y^2}{b^2} = 1$

We are given $|AS_1 - AS_2| = 4 \implies a = 2$ (by a property of hyperbola that you seem to be aware of)

Now I will use two other properties of hyperbola

First: The product of perpendicular distances from foci to any tangent is $b^2$.

So, $d(S_1,PA) \cdot d(S_2,PA) = b^2 \tag1$

Second: The product of perpendicular distances from a point $P$ on the director circle and the center of the hyperbola / director circle to the chord of contact formed by tangents from point $P$ is given by $\frac{a^2b^2}{a^2-b^2}$.

So, $d(P,AB) \cdot d(C,AB) = \frac{a^2b^2}{a^2-b^2} \tag2$

I came to this on my own while working on this problem. I am sure there is literature available showing it but I have not been able to search and find this on the internet yet. See at the end of the answer for further details and how to go about a proof.

It is given that $d(P,AB).d(C,AB)=4d(S_1,PA).d(S_2,PA)$

$\implies b = \sqrt3$

So we have the equation of hyperbola as,

$\displaystyle \frac{X^2}{4}-\frac{Y^2}{3} = 1$

Now to find the equation of hyperbola in the original coordinate system, we look at a few other information provided in the question.

One of the branches of hyperbola is entirely in first quadrant and $y = 4$ intersects it only once. Then one of the asymptotes has to be parallel to x-axis given that the center of the hyperbola is $(1, 2)$. As asymptote passes through the center, we conclude that $y = 2$ is one of the asymptotes. This asymptote got transformed to $Y = - \frac{\sqrt3}{2}X$ in the new coordinates system $XY$.

From here on, it is just series of boring steps using rotation and translation back to original coordinate system to finally obtain the equation of hyperbola as,

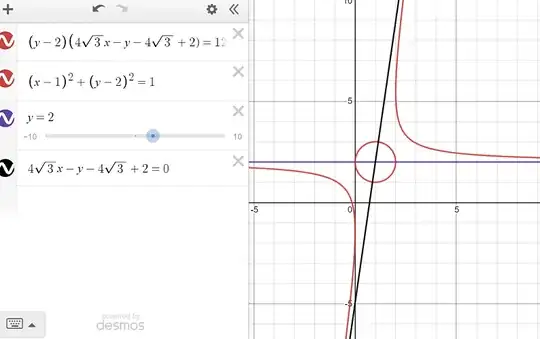
$ \large (y-2) (4 \sqrt3 x - y - 4 \sqrt3 + 2) = 12$

See below for additional info.

---

Here is a plot and certain info using desmos and WolframAlpha.

Now what if you are not convinced on $(1)$ and $(2)$ and want to prove it. By the way, there is enough literature easily available that shows $(1)$.

For $(1)$, take equation of a tangent to hyperbola at point $(X_0, Y_0)$ which is given by $\displaystyle \frac{X X_0}{a^2} - \frac{YY_0}{b^2} = 1$ and find perpendicular distance to this line from points $(\pm ae, 0)$ and multiply it. Using the fact that $\displaystyle \frac{X_0^2}{a^2} - \frac{Y_0^2}{b^2} = 1$, you should be able to show it.

For $(2)$, you know that director of circle is given by $X^2 + Y^2 = a^2 - b^2$. Take a point $P (X_1, Y_1)$ satisfying this equation and draw pair of tangents and then chord of contacts $AB$ to hyperbola from external point $P$ is given by,

$\displaystyle \frac{X X_1}{a^2} - \frac{YY_1}{b^2} = 1$

Find distance to $AB$ from $(X_1, Y_1)$ and $(0, 0)$ and take their product. Using the fact that $(X_1, Y_1)$ satisfies $X_1^2 + Y_1^2 = a^2 - b^2$, you should be able to prove it.

Answer 2

Claim: Assuming a hyperbola has a (real) director circle and satisfies $d(P,AB)\cdot d(C,AB)=K\cdot d(S_1,PA)\cdot d(S_2,PA)$ for all $P$ on the director circle ($A,B,C,S_1,S_2$ same definition as in question, $K$ is a constant), then the semimajor axis $a$ and the semi-minor axis $b$ are related by $$ \frac{b^2}{a^2}=\frac{K-1}{K}. $$

Proof: Choose Cartesian coordinates $(x',y')$ so the hyperbola is $$ \frac{x'^2}{a^2}-\frac{y'^2}{b^2}=1,\quad a>b. $$ Its director circle is $x'^2+y'^2=a^2-b^2$. Pick point $P$ to be $(x'_P,y'_P)=(\sqrt{a^2-b^2},0)$. The tangents from $P$ to the hyperbola is $y'=\pm (x'-x'_P)$. This gives the points $A,B$ are on $x'=\frac{a^2}{x'_P}$. We also know the foci $S_1,S_2$ are $(\pm\sqrt{a^2+b^2},0)$, so feeding that in $d(P,AB)d(C,AB)=Kd(S_1,PA)d(S_2,PA)$ we have $$ \left\lvert x'_P-\frac{a^2}{x'_P}\right\rvert\cdot\frac{a^2}{x'_P}=K\frac{\lvert x'_P-\sqrt{a^2+b^2}\rvert}{\sqrt2}\cdot\frac{\lvert x'_P+\sqrt{a^2+b^2}\rvert}{\sqrt2} $$ yielding the stated relation upon simplification. QED.

Everything else should follow after noting the comments above.