0

Define, with $x$ real valued: $$ F_N(x) = \prod_{k=0}^N\left|x-\frac{k}{N}\right|^{1/N} $$ We can calculate the limit for $N\to\infty$ as a Riemann sum converging to an integral: $$ F_\infty(x) = \lim_{N\to\infty} \prod_{k=0}^N\left|x-\frac{k}{N}\right|^{1/N} = \\ \lim_{N\to\infty} \exp\left[\frac{1}{N}\sum_{k=0}^N\ln\left|x-\frac{k}{N}\right|\right] = \\ \exp\left[\int_0^1\ln|x-t|dt\right] \quad \Longrightarrow \\ F_\infty(x) = \exp\left[(x-1)\ln|x-1| + x\ln|x|-1\right] $$ It can easily be shown that $\,F_\infty(0)=F_\infty(1)=1/e\,$ and there is a minimum for $\,F_\infty(1/2)=1/e/2\,$.
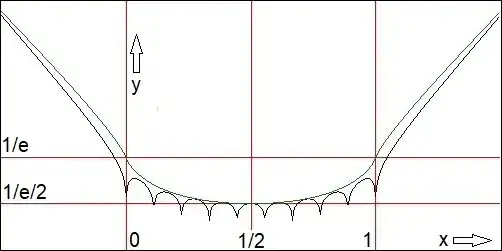
A graph says more than a thousand words:

enter image description here

The interval $\,[0,1]\,$ and the minimum of $\,F_\infty\,$ are delimited with red lines. A sample function $\,F_N(x)\,$ for $\,N=9\,$ is displayed in black. The limit function $\,F_\infty(x)\,$ is displayed in green. Numerically it is suggested that the black curves $\,F_N\,$ converge to the green curve $\,F_\infty\,$.
With exception, though, of the function values $\,f_N(k/N)\,$; all of these must be zero from the start. But in the limit this would mean that $\,F_\infty(x)\,$ is zero as well as non-zero at the whole $\,[0,1]\,$ interval. Which is of course impossible.
What is a sensible way out of this dilemma?

Han de Bruijn
  • 17,475
  • 2
    questions exactly like this are being asked repeatedly on this forum , is this a question from an ongoing contest. ? – Sukhoi234 Aug 24 '21 at 18:10
  • I'm not sure since I don't have a proof, but I think the answer to your dilemma is simple: the product doesn't converge. – jjagmath Aug 24 '21 at 18:10
  • 1
    A little tantrum: I am a weak red-green colorblind and it is almost impossible to distinguish the colors used in the figure. (I can perceive that those curves have different colors, but can't tell which one is red or green.) – Sangchul Lee Aug 24 '21 at 19:09
  • @SangchulLee: Oh well, you’re not too colorblind to formulate a decent (+1) answer :) – Han de Bruijn Aug 24 '21 at 20:17
  • @Sukhoi234: No, this was made up by myself around 2008. Don’t know if it is in some contest, – Han de Bruijn Aug 24 '21 at 20:30
  • Function behaviour and logarithmic differentiation: $$ f_N(x) = \prod_{k=0}^N \left|x-\frac{k}{N}\right|^{1/N} \ \ln\left[f_N(x)\right] = \frac{1}{N} \sum_{k=0}^N \ln\left|x-\frac{k}{N}\right| \ \frac{f'N(x)}{f_N(x)} = \frac{1}{N} \sum{k=0}^N \frac{1}{x-k/N} $$ – Han de Bruijn Sep 13 '21 at 13:17
  • Very interesting and seemingly related: Can we prove AM-GM Inequality using these integrals? Especially this jewel of a formula: $$ \sum_{k=0}^{n-2}\frac{1}{\pi}\sin \tfrac{\pi (k+1)}{n}\int_{a_k}^{a_{k+1}} \left(\prod_{i=0}^{n-1}\sqrt[n]{|x-a_i|}\right)\frac{dx}{x} =\frac{1}{n}\sum_{i=0}^{n-1}a_i - \sqrt[n]{\prod_{i=0}^{n-1}a_i} $$ – Han de Bruijn Sep 19 '21 at 17:41

1 Answers1

1

The answer is simple: $F_N(x)$ does not converge to $\exp\left(\int_{0}^{1}\log|x-t|\,\mathrm{d}t\right)$ when $x \in \mathbb{Q}\cap[0,1]$.

Let $x \in [0, 1]$. Then it is not hard to check that

$$ \log F_N(x) = \int_{0}^{1} \log|x-t| \, \mathrm{d}t + \frac{1}{N} \log\operatorname{dist}\biggl( x, \frac{1}{N}\{0,1,\ldots,N\} \biggr) + \mathcal{O}\biggl( \frac{\log N}{N} \biggr). $$

So, $\log F_N(x)$ converges to $\int_{0}^{1} \log|x-t| \, \mathrm{d}t$ if and only if

$$ \liminf_{N\to\infty} \frac{1}{N} \log\operatorname{dist}\biggl( x, \frac{1}{N}\{0,1,\ldots,N\} \biggr) = 0. $$

Equivalently, $\log F_N(x)$ does not converge to $\int_{0}^{1} \log|x-t| \, \mathrm{d}t$ if and only if

$$ x \in A := \bigcap_{p=1}^{\infty}\bigcap_{N=1}^{\infty}\bigcup_{n=N}^{\infty}\bigcup_{k=0}^{n} \biggl( \frac{k}{n}-e^{-n/p}, \frac{k}{n}+e^{-n/p}\biggr). $$

It is also interesting to note that $A$ is a $G_{\delta}$-set containing $\mathbb{Q}\cap[0,1]$, hence is uncountable.

Sangchul Lee
  • 181,930