Hints:
$~$ If $(u_n)$ is a sequence in a normed space $X$ such that $u_n $ converges weakly to some $u \in X$ then there exists a sequence $(v_n)$ in $X$ with $v_n \in \operatorname{conv} \{ u_1,u_2, \dots \}$ such that $v_n \to u$.
If $f_n \to f$ in $L^p$ then there exists a subsequence of $f_n$ that converges a.e. to $f$.
Edit: The proof of 1. uses Mazur's theorem. Let $C= \operatorname{conv} \{ u_1,u_2,\dots \}$ (the convex hull of $(u_n)$). Note that $u \in \overline{C}^w$, the weak closure of $C$, since $u_n \to u$ weakly, and that $C$ is convex. By Mazur's theorem we have that $\overline{C} = \overline{C}^w$ and so $x \in \overline{C}$. This then implies the existence of a sequence $(v_n)$ in $C$ that converges to $u$ in the norm topology.
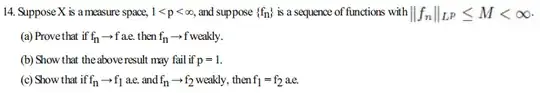
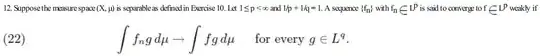 Does anyone know how to prove $(c)$ part
Does anyone know how to prove $(c)$ part