This question concerns a generalization of the following problem (allegedly, in the early days of Tesla and SpaceX, Elon Musk would ask the following question to possible future employees):
Assume that you are standing on the surface of the Earth and that Earth's surface is perfectly spherical. Find the set of points such that walking $1~\mathrm{km}$ South, $1~\mathrm{km}$ West then $1~\mathrm{km}$ North brings you back to the same position.
In case you would like to try and solve this puzzle yourself, I hide the solution below:
There are infinitely many points which satisfy this condition. The obvious solution is the North pole. The other set of solutions are the set of points $1~\mathrm{km}$ North of the circles of circumference $1/n~\mathrm{km}$ around the South pole for all $n\in \mathbb{N}$. If my explanation is unclear, see for instance this YouTube video.
I would like to generalize this problem further:
Assume that you are standing on the surface of the Earth and that Earth's surface is perfectly spherical. Find the set of points such that walking $x~\mathrm{km}$ at a bearing of $\alpha^{\circ}$, $y~\mathrm{km}$ at a bearing of $\beta^{\circ}$ then $z~\mathrm{km}$ at a bearing of $\gamma^{\circ}$ brings you back to the same position.
The main focus of this question is to obtain this locus. So far I know the following:
Suppose you start from the surface of the Earth of radius $R$ at latitude/longitude $(\varphi_1,\lambda_1)$ and walk a (rhumb line, not geodesic) distance $d$ at a constant bearing $\theta$. Then it can be shown that the latitude $\varphi_2$ and longitude $\lambda_2$ after walking this distance is (normalize to $\varphi_{1,2}\in [-\pi/2,\pi/2]$ and $\lambda_{1,2}\in [-\pi,\pi)$ if necessary) $$\varphi_2=\varphi_1+\frac{d}{R}\cos(\theta),$$ $$\lambda_2=\lambda_1+\frac{d}{R}\cdot \frac{\sin(\theta)}{q},$$ where $$q:=\begin{cases} \frac{\varphi_2-\varphi_1}{\ln(\tan(\varphi_2/2+\pi/4)/\tan(\varphi_1/2+\pi/4))},&\mathrm{if}~\theta\not\in \{\pi/2,3\pi/2\}, \\ \cos(\varphi_1),&\mathrm{otherwise}. \end{cases}$$ Hence, we are asking for fixed points of the function $f_{z,\gamma}\circ f_{y,\beta}\circ f_{x,\alpha}$ where $f_{d,\theta}$ is defined as $$f_{d,\theta}(\varphi_1,\lambda_1)=(\varphi_2,\lambda_2)$$ where $\varphi_2$ and $\lambda_2$ are as above. The problem is that I do not think it is easy to solve for the fixed points. I also thought about solving such an equation numerically. However, since we are generally dealing with infinitely many solutions (I am not sure if there are special cases with finitely many points), it will be quite difficult to use a root finding method (e.g. Newton-Raphson).
Hence, my question is:
Given any $x,y,z,\alpha,\beta$ and $\gamma$ is there any way to compute the set of solutions either analytically (an approximate locus is also acceptable) or via some computational methods?
UPDATE: Recently I had the idea of using Mathematica to find the locus. Here I define a function RhumbSeqDiff, which computes the norm of the differences between the initial and final latitudes and longitudes after walking the given distances (to test if the program works, I use the parameters in the simplified problem).
R = 6371;
x = 1;
y = 1;
z = 1;
alpha = 180;
beta = 270;
gamma = 0;
Rhumb[Phi1_, Lambda1_, Theta_, d_] :=
({Phi1Rad = Phi1*(Pi/180);
Lambda1Rad = Lambda1*(Pi/180);
ThetaRad = Theta*(Pi/180);
Phi2Rad = Phi1Rad + (d/R)*Cos[ThetaRad];
DeltaPsi =
Log[Tan[(Phi2Rad/2) + (Pi/4)]/Tan[(Phi1Rad/2) + (Pi/4)]];
q = If[Theta == 90 || Theta == 270,
Cos[Phi1Rad], (Phi2Rad - Phi1Rad)/DeltaPsi];
DeltaLambda = (d/R)*(Sin[ThetaRad]/q);
Lambda2Rad = Lambda1Rad + DeltaLambda;
Phi2Deg = Phi2Rad*(180/Pi),
Lambda2Deg = Mod[Lambda2Rad*(180/Pi) + 540, 360] - 180});
RhumbSeq[Phi1_, Lambda1_] :=
Rhumb[Part[
Rhumb[Part[Rhumb[Phi1, Lambda1, alpha, x], 1],
Part[Rhumb[Phi1, Lambda1, alpha, x], 2], beta, y], 1],
Part[Rhumb[Part[Rhumb[Phi1, Lambda1, alpha, x], 1],
Part[Rhumb[Phi1, Lambda1, alpha, x], 2], beta, y], 2], gamma, z];
RhumbSeqDiff[Phi1_, Lambda1_] :=
Norm[RhumbSeq[Phi1, Lambda1] - {Phi1, Lambda1}];
I decided to see if the function would work if we select the solutions on the South Pole. Using some simple trigonometry, one finds that the latitudes of these solutions (in degrees) are
$${\varphi_n}^{\circ}=-\frac{180}{\pi}\arccos\left(\frac{1}{2\pi R n}\right)+\frac{360}{2 \pi R},\quad \forall n\in \mathbb{N}.$$
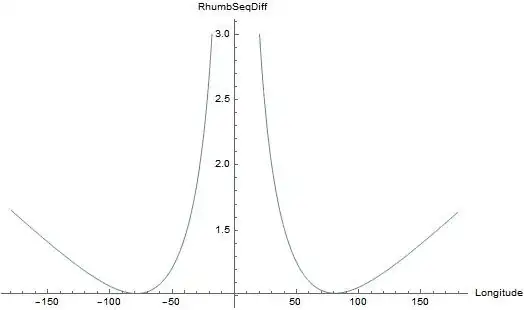
I tested if RhumbSeqDiff[-(180/Pi)*ArcCos[1/(2*R*Pi)] + 360/(2*R*Pi), lambda] would return $0$ for any lambda, which is what happened - as expected. However, when I try to plot the function I get some weird results. For instance, if I plot the function along the $n=1$ solution using Plot[RhumbSeqDiff[-(180/Pi)*ArcCos[1/(2*R*Pi)] + 360/(2*R*Pi), x], {x, -180, 180}], I get dependence on $\lambda$ and the function is nonzero everywhere:
My idea was that I could use ContourPlot or RegionPlot to find the locus (such as ContourPlot[RhumbSeqDiff[y,x]==0, {x, -180, 180},{y, -90, 90}]), but with this bug I am unable to do so. Perhaps this problem is rectifiable?