Regarding topic: SE I encountered a convolution of two identical $\arcsin$ distributions. The probability density function $pdf$ for $R \in [−1,1]$ in this context is:
$$f(R)=\frac{1}{\pi \sqrt{1-R^2}}$$
The convolution of two $\arcsin$ pdf's would then be (not sure if this is allowed):
$$f(R)*f(R)= \int_{-a}^{a} \frac{1}{\pi \sqrt{1-\tau^{2}}} \cdot \frac{1}{\pi \sqrt{1-(R-\tau)^{2}}} d \tau$$
Wolfram Alpha online gives a complicated formula (without integral limits) as a solution:
$$f(R)*f(R)=$$ $$\small{ \left[- \frac{2(\tau-1)(\tau+1) \ \sqrt{ \frac{\tau - R+1}{( \tau -1) R)}} \ \sqrt{ \frac{\tau - R-1 }{(\tau-1) ( R +2)}} \ F \left[ \arcsin \left( \sqrt{\frac{(\tau+1) R}{(\tau-1) (R+2)} } \right), 1 - \frac{4}{R^2} \right] }{\pi^2 \sqrt{1 - \tau^2} \sqrt{ \frac{(\tau+1) R}{( \tau-1) (R+2)}} \sqrt{- \tau^2 + 2 \tau R - R^2 + 1} } \right]_{-a}^{a} }$$
Here the elliptic integral $F(\lambda,m)$ (incomplete first kind) occurs. I have little experience in convolution and elliptic integrals.
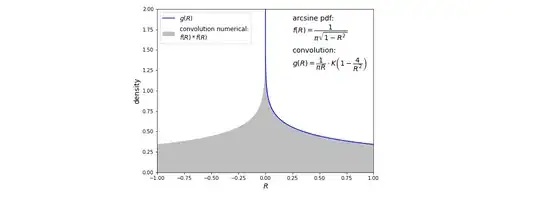
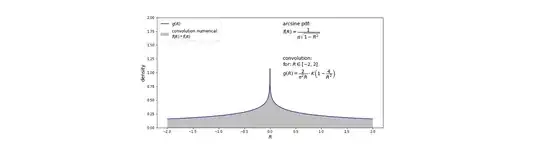
I studied and did some empirical trial and error investigation. I calculated the convolution numerical and guessed the equation fitting the numerical convolution.
First, I took the limit for $\tau \to \infty$ from solution Wolfram Alpha giving:
$$\frac{2}{\pi^2 R} \ F \left[ \arcsin \left( \sqrt{\frac{ R}{R+2} } \right), 1 - \frac{4}{R^2} \right] $$
Then after trial and error I noticed multiplying with $\pi /2$ gives correct scaling with numerical convolution (see graph).
After study SE I found that the incomplete elliptic integral $F(\lambda,m)$ can be replaced by a complete elliptic integral $K(m)$ for real parts solution.
So, my empirical found $pdf$ for the convolution of two $\arcsin$ distributions describing half the $pdf$:
EDIT: This far I got lucky guessing with trial and error. Next formula is not correct. See comments and answers.
$$\boxed{g(R)= \dfrac{1}{\pi R} \cdot K \left[ 1- \dfrac{4}{R^{2}} \right]}$$
My method is very intuitive and am looking for more rigorous proof. I do not understand all steps I have done. My skill level is amateur/hobby hoping to find fitting comments/answers.
Mystery's:
- What limits for the convolution integral should be taken?
- Why does multiplying with $\pi /2$ give correct scaling?
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import ellipk
fig, ax = plt.subplots(1, figsize=(12,6))
#Numerical Convolution Arcsine
R=np.linspace(-0.9999999,0.9999999,100000)
dR=R[1]-R[0]
arcsin=1/(np.pi(np.sqrt(1-R2)))
pdf=np.convolve(arcsin,arcsin,mode='same')
size=np.size(pdf)
af=dRnp.sum(pdf)
f2=pdf/af
f1=np.full(np.size(pdf),0)
ax.fill_between(R[::10], f1[::10], f2[::10],color='black',zorder=-10,alpha=0.25,label="convolution numerical:\n$f(R)*f(R)$",interpolate=True,linewidth=0)
#Formula convolution with Elliptic Integral
R1=np.linspace(0.00000001,1,1000)
f3b=ellipk(1-4/(R1*2))
f3b=1/(np.piR1)*f3b
ax.plot(R1,f3b,label=r"$g(R)$",color='blue',linewidth=1.5)
text="arcsine pdf: \n" + r"$f(R)= \dfrac{1}{\pi \sqrt{1-R^2}}$"
ax.text(0.25,1.7,text,fontsize=14)
text="convolution: \n" + r"$g(R)= \dfrac{1}{\pi R} \cdot K \left( 1- \dfrac{4}{R^{2}} \right)$"
ax.text(0.25,1.3,text,fontsize=14)
ax.set_xlabel("$R$",fontsize=14)
ax.set_ylabel("density",fontsize=14)
ax.legend(loc="upper left",fontsize=12)
ax.set_xlim([-1, 1])
ax.set_ylim([0,2])
plt.show()
$$\Bigg[- \frac{2(\tau-1)(\tau+1) \ \sqrt{ \frac{\tau - R+1}{( \tau -1) R)}} \ \sqrt{ \frac{\tau - R-1 }{(\tau-1) ( R +2)}} }{\pi^2 \sqrt{1 - \tau^2} \sqrt{ \frac{(\tau+1) R}{( \tau-1) (R+2)}} \sqrt{- \tau^2 + 2 \tau R - R^2 + 1} }\Bigg]^2=\frac{4}{\pi ^4 R^2}$$
– Claude Leibovici Aug 02 '21 at 03:19