4

For a given wallpaper symmetry group, it seems like there should be a minimal set of group element relations that generate the symmetry group. For example, the p1 symmetry group only has translational symmetry, so I can say that the group is generated by the elements $T_x$ and $T_y$, with the relation $T_x T_y T_x^{-1} T_y^{-1} = 1$. I would like to know if such a description exists for the other 16 wallpaper groups. Clearly for a given symmetry group, I could write down all the various transformations in that group (translations, reflections, rotations, glide reflections, etc.) and start pairing up different transformations to derive various relations, but it's not clear to me at what point my list of relations become necessary and sufficient for specifying the wallpaper group under consideration.

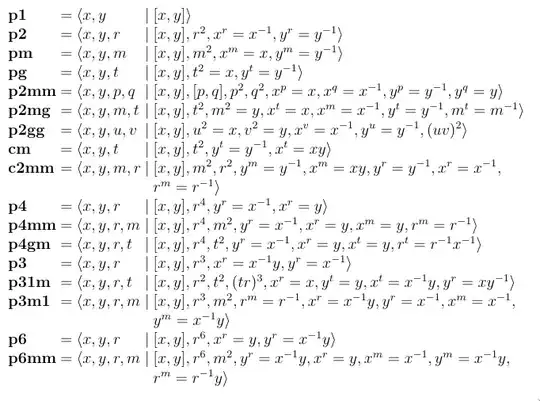
The closest question I've found to this is here, but the answer refers to a thesis written in German so I can't fully understand it. There is a section from the referenced thesis that seems relevant to my question, which seems to specify the symmetry groups in terms of group relations: enter image description here

but as far as I can tell, gives no indication of what the variables correspond to in terms of concrete symmetry transformations (except for $x$ and $y$, which I'm assuming are translations).

Henry Shackleton
  • 273
  • 1
    As the thesis you mentioned states, these appear to be given in Coxeter-Moser's work 'Generators and relations for discrete groups'. – David A. Craven Jul 30 '21 at 19:08
  • Given that $x$ and $y$ are generators for the translation group, you should also be able to deduce what the other generators are from their actions on the translations. For example, in p2, $r$ inverts both translations by conjugation and has order $2$, so that immediately tells you what it is. Whereas in pm, $m$ inverts one and centralizes the other. And so on. – David A. Craven Jul 30 '21 at 19:20

0 Answers0