How to solve $\tan^2x + \tan^2{2x} + \cot^2{3x} =1$?
I've tried to use some formulas and I've written that 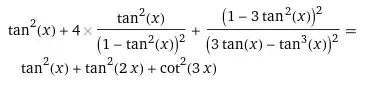
but it didn't make much easier. The derivative is ugly too.
Mayby there is a simple way?
How to solve $\tan^2x + \tan^2{2x} + \cot^2{3x} =1$?
I've tried to use some formulas and I've written that 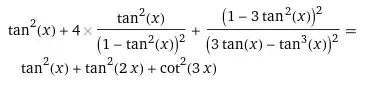
but it didn't make much easier. The derivative is ugly too.
Mayby there is a simple way?
Let $u = \tan(x)$.
Using the equation you found, we can write:
$u^2 + \frac{4u^2}{(1-u^2)^2} + \frac{(1-3u^2)^2}{(3u - u^3)^2} = 1$
Simplifying, we get:
$u^{12} - 9 u^{10} + 43 u^8 - 94 u^6 + 91 u^4 - 17 u^2 + 1 = 0$
Finding the Sturm chain of the above polynomial, we see that there is no change in sign, thus implying that there are no real roots to the above equation.