I'm following an example from Nonlinear Dynamics and Chaos (Strogatz) that asks to show how if $f$ has a stable $p$-cycle then the Lyapunov exponent $\lambda<0$. I understand why this must be the case, and I follow the maths detailed in the example except for this part:
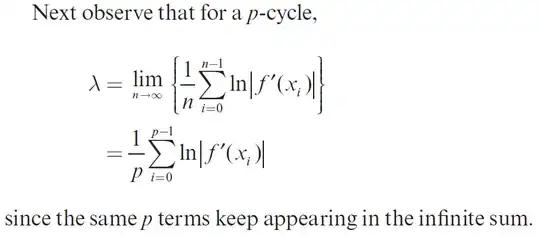 How does the limit resolve and $p$ is made part of the equation? I understand it has something to do with the orbit being periodic, but I need to see some more steps going from the term involving the limit to the term without.
How does the limit resolve and $p$ is made part of the equation? I understand it has something to do with the orbit being periodic, but I need to see some more steps going from the term involving the limit to the term without.
1 Answers
I'll use the notation I introduced in my answer https://math.stackexchange.com/a/4204125/169085 to your previous question. Thus if $f:X\to X$ is continuously differentiable and $x\in X$, I parameterize the orbit of $x$ under (iterates of) $f$ by $x_\bullet:\mathbb{Z}_{\geq0}\to X, n\mapsto f^n(x)$. It seems this is also in accordance with Strogatz' notation.
Let's start with some more notation. Most of this is not needed for your question, but I believe you may find the framework useful when studying dynamics.
$x\in X$ is a fixed point of $f$ if $f(x)=x$. $x\in X$ is a periodic point of $f$ if for some $n\in\mathbb{Z}_{\geq1}$ it is a fixed point of $f^n$. Note that as we discussed in your previous question $f^n:X\to X$ is a map in and of itself. If $m$ and $n$ are two positive integers, and $m$ is a multiple of $n$, then any fixed point of $f^n$ is also a fixed point of $f^m$, but of course the converse is not true in general. Because of this for $p\in\mathbb{Z}_{\geq1}$ let us call $x\in X$ a periodic point of $f$ of minimal period $p$ if $x$ is a fixed point of $f^p$ but not a fixed point of $f^k$ for any $k\in\{1,2,...,p-1\}$ (there is some redundancy in the range of $k$ due to divisibility matters I mentioned above). The orbits of fixed points of $f$ are singletons and more generally the orbits of periodic points of $f$ are finite sets. I believe what Strogatz calls a $p$-cycle is the orbit of a periodic point of $f$ of minimal period $p$. Let me also mention that "prime period" is also used at times instead of "minimal period", but of course this does not mean that $p$ is a prime number.
I'll denote by $\operatorname{Fix}(f)$ the set of fixed points of $f$, by $\operatorname{Per}(f)$ the set of periodic points of $f$ and for $p\in\mathbb{Z}_{\geq1}$ by $\operatorname{Per}_p(f)$ the set of periodic points of $f$ of minimal period $p$. Thus the previous paragraph is summarized by:
\begin{align*} \operatorname{Fix}(f) &= \{x\in X| f(x)=x\}\\ \operatorname{Per}(f) &= \bigcup_{n\in\mathbb{Z}_{\geq1}} \operatorname{Fix}(f^n)\\ \forall p\in\mathbb{Z}_{\geq1}: \operatorname{Per}_p(f) &= \operatorname{Fix}(f^p)\setminus \bigcup_{k=1}^{p-1} \operatorname{Fix}(f^k). \end{align*}
There are further relations between these sets; I'll leave them to you to think about. Likewise these notions generalize without much hassle to continuous time dynamical systems. Also observe that none of these notions require differentiability, nor indeed continuity. (Once topology is involved there are more sophisticated sets one can attach to $f$ that carry more robust recurrence information, e.g. the recurrent set or the nonwandering set. Here topology is involved, but I still won't go any further, as I believe again the question is mainly about notation.)
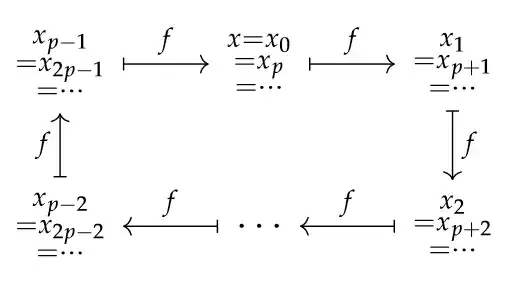
If $x\in \operatorname{Per}_p(f)$, then the orbit of $x$ under $f$ is:
$$\{x, f(x), f^2(x),..., f^{p-1}(x)\}= \{x=x_0,x_1,...,x_{p-1}\},$$
and there are no repetitions, so that this set has exactly $p$ elements. Our orbit parameterization $x_\bullet: \mathbb{Z}_{\geq0}\to X$ still holds, but there is some redundancy with indices. More precisely:
$$\forall q\in \mathbb{Z}_{\geq0},\forall r\in\{0,1,...,q-1\}: x_{qp+r}=x_r.$$
(I'm leaving this to you to verify.)
Here is a humble graphical representation:
Next, some observations about integers. Fix $p\in\mathbb{Z}_{\geq0}$ (this'll be the minimal period).
Obs.1: For any $n\in\mathbb{Z}_{\geq0}$, there is a unique $q=q_n\in\mathbb{Z}_{\geq0}$ and a unique $r=r_n\in\{0,1,...,p-1\}$ such that $n= q_n p + r_n$ ($q$ for "quotient" and $r$ for "residue"; they also depend on $p$ of course, but we won't fiddle with $p$ for the purposes of the limit in question). I'll leave this to you too; the point is that one can think of $q$ as the unit measurement (of time, in the context of dynamics), so multiples of $q$ partition of $\mathbb{Z}_{\geq0}$ into sets of equal size (I find it useful to draw a picture to see this).
Obs.2: More importantly for our purposes, we have:
$$\lim_{n\to\infty} \dfrac{q_n}{n}=\dfrac{1}{p},\quad \lim_{n\to\infty}\dfrac{r_n}{n}=0.$$
(Yours.)
Obs.3: We can split a sum we take over $\{0,1,...,n\}$ accordingly. More precisely, using $a_\bullet:\mathbb{Z}_{\geq0}\to\mathbb{R}$ as anonymous terms,
\begin{align*} \sum_{i=0}^n a_i &= \sum_{i=0}^{p-1} a_i+\sum_{i=p}^{2p-1}a_i+ \cdots +\sum_{i=(q_n-1)p}^{q_np-1}a_i+\sum_{i=q_np}^{q_np+r_n}a_i\\ &=\sum_{j=0}^{q_n-1}\sum_{i=jp}^{(j+1)p-1}a_i+\sum_{i=q_np}^{q_np+r_n}a_i\\ &=\sum_{j=0}^{q_n-1}\sum_{i=0}^{p-1}a_{jp+i}+\sum_{i=0}^{r_n}a_{q_np+i}. \end{align*}
Obs.4: If in addition $a_\bullet$ is $p$-periodic, that is, $a_{\bullet+p}=a_\bullet$, then this last formula reduces to
\begin{align*} \sum_{i=0}^n a_i =\sum_{j=0}^{q_n-1}\sum_{i=0}^{p-1}a_{i}+\sum_{i=0}^{r_n}a_{i} =q_n\sum_{i=0}^{p-1}a_{i}+\sum_{i=0}^{r_n}a_{i}. \end{align*}
Note that here $\sum_{i=0}^{p-1}a_{i}$ is a fixed number (i.e. is independent of $n$) and $n\mapsto\sum_{i=0}^{r_n}a_{i}$ is bounded from above by $M=\max_{s\in\{0,1,...,p-1\}}\left(\sum_{i=0}^{s}a_{i}\right)$ (and similarly from below by the analogous minimum).
For completeness let's also recall the definition of the (top) Lyapunov exponent of $f$. For $x\in X$, the (top) Lyapunov exponent of $f$ at $x$ is the (extended) number $\lambda_x(f)\in[-\infty,\infty[$ (it could take the value $-\infty$, as in the second part of the example (= Ex.10.5.1 on p.374 for the second edition) you are referring to in Strogatz' book) defined by
$$\lim_{n\to\infty}\dfrac{\ln |(f^n)'(x)|-\lambda_x(f)\, n}{n}=0 $$
(whenever this limit exists; otherwise one replaces $\lim$ with $\limsup$). We know after your previous question that
$$\lambda_x(f) = \lim_{n\to\infty}\dfrac{1}{n}\ln |(f^n)'(x)|= \lim_{n\to\infty}\dfrac{1}{n}\sum_{i=0}^{n-1}\ln |f'(x_i)|.$$
Let me note that the parenthetical adjective "(top)" refers to what Strogatz refers to on p. 329: in general this formula gives the largest Lyapunov exponent of $f$ (and there could be as many distinct Lyapunov exponents as the dimension of the manifold $X$). In this regard it is instructive to compare this to Gelfand's formula.
Now let's assemble all this to get the dynamical statement. Fix $p\in\mathbb{Z}_{\geq1}$ and $x\in \operatorname{Per}_p(f)$. Then
\begin{align*} \lambda_x(f) &= \lim_{n\to\infty}\dfrac{1}{n}\sum_{i=0}^{n-1}\ln |f'(x_i)| = \lim_{n\to\infty}\dfrac{1}{n}\left(q_n\sum_{i=0}^{p-1}\ln |f'(x_i)|+\sum_{i=0}^{r_n}\ln |f'(x_i)|\right)\\ &= \left(\lim_{n\to\infty}\dfrac{q_n}{n}\right)\sum_{i=0}^{p-1}\ln |f'(x_i)|+\lim_{n\to\infty}\dfrac{\text{bounded}}{n} =\dfrac{1}{p}\sum_{i=0}^{p-1}\ln |f'(x_i)|, \end{align*}
where the second equality is due to Obs.4 and the last equality is due to Obs.2. Note that we didn't use the stability of $x$ in none of this.
Here is an interpretation of this: put $\Phi_f: X\to \mathbb{R}, x\mapsto \ln|f'(x)|$. Note that as $f$ is continuously differentiable $\Phi_f$ will be continuous. Then the (top) Lyapunov exponent of $f$ at a periodic point is precisely the (time) average of $\Phi_f$ over the orbit of said point. $\Phi_f$ goes by the name of the geometric potential of $f$ (typically when $|f'|>1$).
- 12,209