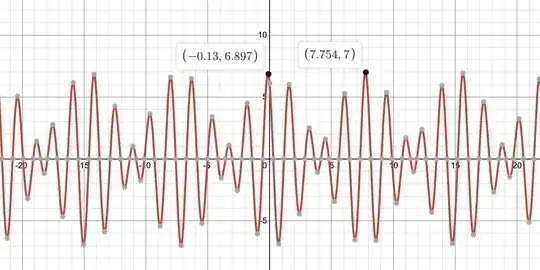
(I had asked in this question how should I begin to add together these two trigonometric functions: $z(t) = 3\cos(3t + \pi/5) + 4\cos(4t+\pi/8)$, in order to obtain the period of their sum). Now, I wonder how I might do so, should the angular frequency of the first be altered from $3$ to $\sqrt{10}$: $$z(t) = 3\cos\left(\sqrt{10}t + \frac\pi5\right) + 4\cos\left(4t+\frac\pi8\right)$$
which I think to be considerably more difficult, for obeys no longer the relation $z(t+2π) = z(t)$.