Is there an exact solution for $\large\int \frac{dx}{\tan^{-1}(x)}$?

Question

Do you know about the inverse tangent integral function? It is defined as: $$\mathrm{Ti_2(x)=Ti(x)=\int_0^x\frac{tan^{-1}(x)}{x}dx=-\frac1x\sum_{n\ge 1}\frac{(-1)^nx^{2n}}{(2n-1)^2}}$$

Expanding the denominator and then the sum gives many other forms of the function. Also, I wondered what other unsolved trigonometric integrals there are. You can click my profile questions to see similar inspiration questions. Here is the function I want to find. Here is an interactive graph. It is an odd injective function:

$$\mathrm{T(x)=\int \frac{dx}{tan^{-1}(x)} , \\ T(b)-T(a)=\int_a^b \frac{dx}{tan^{-1}(x)}=\int_{tan^{-1}(a)}^{tan^{-1}(b)} \frac{sec^2(x)}{x}dx\mathop=^{|x|<\frac\pi 2} \quad \int_{tan^{-1}(a)}^{tan^{-1}(b)}\sum_{N=0}^\infty\sum_{n=0}^\infty\frac{(-1)^{N+n}E_{2N}E_{2n}x^{2(N+n)-1}}{(2N)!(2n)!}dx= \quad \sum_{N=0}^\infty\sum_{n=0}^\infty\frac{(-1)^{N+n}E_{2N}E_{2n}(tan^{-1}(b))^{2(N+n)}-(tan^{-1}(a))^{2(N+n)}}{2(2N)!(2n)!(N+n)}}$$

This approach above uses the Euler numbers $\mathrm E_y$ and this series representation. This looks very complicated as I had to multiply the two series together to get a secant squared representation.

Here is a solution for T(x), but I do not know the Laurent series coefficient formula:

$$\mathrm{T(x)=\int \sum_{n=0}^\infty c_n x^{2n-1}dx=\int \frac1x +\frac x3-\frac{4x^3}{45}+\frac{44x^5}{945} -\frac{428x^7}{14175}+\frac{10196x^9}{467775}-\frac{10719068x^{11}}{638512875}+…dx=ln(x)+\sum_{n=1}^\infty \frac{c_n x^{2n}}{2n}=ln(x)+\frac {x^2}6-\frac{x^4}{45}+\frac{22x^6}{2835}-\frac{108x^8}{28350}+\frac{5098x^{10}}{2338875}-\frac{2679767x^{12}}{1915538625}+…,c_n=1,\frac13,-\frac4{45},\frac{44}{945},-\frac{428}{14175},\frac{10196}{467775},-\frac{10719068}{638512875},…}$$

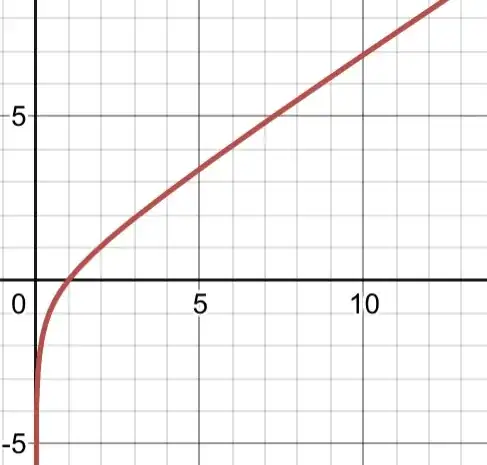
Here is a graph of T(x). Notice the oblique asymptote which is a consequence of the fact that $\frac1{\tan^{-1}(\pm \infty)}=\frac2\pi$. The graph is for the area from x=1 to x=$\text x_0$. You can also see the vertical asymptote at x=0 implying infinite area over almost any interval containing x=0:

Here is motivation using trigonometric integral functions. I will assume a primitive here, no constant, for simplicity:

$$\mathrm{\int\frac{dx}{cos^{-1}(x)}=-Si(cos^{-1}(x))}$$

$$\mathrm{\int\frac{dx}{sin^{-1}(x)}=Ci(sin^{-1}(x)}$$

$$\mathrm{\int\frac{dx}{cosh^{-1}(x)}=Shi(cosh^{-1}(x))}$$

$$\mathrm{\int\frac{dx}{sinh^{-1}(x)}=Chi(sinh^{-1}(x)}$$

Just like the actual inverse tangent integral, I wonder if this T(x) function can also be expressed in exact form. If possible, please express in closed form, but an exact answer also works. I would be surprised if T(x) can even be expressed in terms of Ti(x), the inverse tangent integral.

Another answer is to find out if the coefficients I typed above have any pattern that can be written as an mathematical expression.

Please correct me and give me feedback!

Applications: Try the inverse integral theorem on $\tan\frac1x$ You can try this problem, find the integral $\mathrm{\int_{i}^{2i}\frac{dx}{tan^{-1}(x)}=\int_1^2\frac{i\,dx}{tanh^{-1}(x)}}$, and I will try to ask a question about the applications though .

Results from @Yuri Negometyanov and @Nikos Bagis show the following results. Graphical proof. Note that you can split the sum after distributing the factored numerator. Bernoulli Numbers. Notice the root of the desmos graph at different values. Be sure to set the slider to approach $\pm \infty$ for i by approximation of $\pm 10$ in the graph link:

$$\mathrm{T(x)=\int\frac{dx}{\tan^{-1}(x)}=\frac{x}{\tan^{-1}(x)}+ln\left(\tan^{-1}(x)\right)-\frac12 \sum_{n=2}^\infty\frac{(-4)^n\left(4^n-1\right)B_{2n} \left(\tan^{-1}(x)\right)^{2(n-1)}}{(n-1)(2n)!}+C=ln\left(tan^{-1}(x)\right)+\frac{x}{tan^{-1}(x)}-\frac{4}{\pi^2}\sum_{n\in \Bbb Z}\frac{ln\left(\pi(2n+1)-2tan^{-1}(x)\right)}{(2n+1)^2}+C}$$

I wonder about the integrals of the reciprocal of other inverse trigonometric functions…

Answer 1

Let $$I(x)=\int\limits_1^x \dfrac{\text dt}{\arctan t},\tag1$$ then $$I(\tan y)=\int\limits_{\large^\pi/\mspace{1mu}_4}^y\dfrac1t\,\text d\tan t \;\overset{\text{IBP}}{=\!=}\;\dfrac{\tan t}t\bigg|_{\large^\pi/\mspace{1mu}_4}^y+\int\limits_{\large^\pi/\mspace{1mu}_4}^y\,\dfrac{\tan t}{t^2}\,\text dt = \dfrac{\tan y}y-\dfrac4\pi +\int\limits_{\large^\pi/\mspace{1mu}_4}^y\dfrac{\tan t}{t^2}\,\text dt,\tag2$$ or, applying the known Maclaurin series of the tangent function in the form of $$\tan t =\sum\limits_{n=1}^\infty (-1)^{n-1}\dfrac{4^n(4^n-1)\text B_{2n}}{(2n)!}t^{2n-1}= t+\dfrac13\,t^3+\dfrac2{15}\,t^5+\dfrac{17}{315}\,t^7+\dfrac{62}{2835}\,t^9+\dots,\tag3$$

$$\color{green}{\mathbf{I(\tan y)= \dfrac{\tan y}y-\dfrac4\pi+\ln\dfrac{4y}\pi + \sum\limits_{n=2}^\infty c_n \left(y^{2n-2}-\left(\dfrac\pi4\right)^{2n-2}\right),}}\tag4$$ where $$\color{green}{\mathbf{c_n = (-1)^{n-1}\dfrac{4^n(4^n-1)\text B_{2n}}{(2n-2)(2n)!}.}}\tag5$$

I.e., we have got $\;1D\;$ series.

Alternative form of the solution $(4)$ is $$\color{green}{\mathbf{I(x)= \dfrac x{\arctan x}-\dfrac4\pi+\ln\dfrac{4\arctan x}\pi + \sum\limits_{n=2}^\infty c_n\left(\arctan^{2n-2} x -\left(\dfrac\pi4\right)^{2n-2}\right).}}\tag6$$

Answer 2

It is known that $$ \csc^2 z=\sum^{\infty}_{k=-\infty}\frac{1}{(z-k\pi)^2}\textrm{, }z\neq 0,\pm\pi,\pm 2\pi,\ldots\tag 1 $$ Hence with $z\rightarrow z-\frac{\pi}{2}$, we have $$ \sec^2 z=\sum^{\infty}_{n=-\infty}\frac{1}{(z-\pi/2-k\pi)^2}\tag 2 $$ Also $$ \frac{d}{dt}\int^{\tan t}_{c}\frac{1}{\arctan x}dx=\frac{\sec^2 t}{t} $$ Hence using (1): $$ I=\int^{\tan t}_{c}\frac{1}{\arctan x}dx= $$ $$ =\sum _{k=-\infty }^{\infty } [\frac{4 \pi }{(\pi +2 k \pi )^2 (\pi +2 k \pi -2 t)}+\frac{8 k \pi }{(\pi +2 k \pi )^2 (\pi +2 k \pi -2 t)}- $$ $$ -\frac{4 \pi \log(\pi +2 k \pi -2 t)}{(\pi +2 k \pi )^2 (\pi +2 k \pi -2 t)}-\frac{8 k \pi \log(\pi +2 k \pi -2 t)}{(\pi +2 k \pi )^2 (\pi +2 k \pi -2 t)}+ $$ $$ +\frac{8 t \log(\pi +2 k \pi -2 t)}{(\pi +2 k \pi )^2 (\pi +2 k \pi -2 t)}+\frac{4 \pi \log(2 t)}{(\pi +2 k \pi )^2 (\pi +2 k \pi -2 t)}+ $$ $$ +\frac{8 k \pi \log(2 t)}{(\pi +2 k \pi )^2 (\pi +2 k \pi -2 t)}-\frac{8 t \log(2 t)}{(\pi +2 k \pi )^2 (\pi +2 k \pi -2 t)}]+C. $$ But $$ S_1=\sum^{\infty}_{k=-\infty}\frac{4\pi}{(\pi+2k\pi)^2(\pi+2 k\pi-2t)}=\frac{\pi (-t+\tan t)}{2 t^2} $$ $$ S_2=\sum _{k=-\infty }^{\infty } \frac{8 k \pi }{(\pi +2 k \pi )^2 (\pi +2 k \pi -2 t)}=\frac{\pi t-\pi \tan t+2 t \tan t}{2 t^2} $$ $$ S_3=\sum _{k=-\infty }^{\infty } \frac{4 \pi \log (2 t)}{(\pi +2 k \pi )^2 (\pi +2 k \pi -2 t)}=\frac{\pi \log(2 t) (-t+\tan t)}{2 t^2} $$ $$ S_4=\sum _{k=-\infty }^{\infty } \frac{8 k \pi \log(2 t)}{(\pi +2 k \pi )^2 (\pi +2 k \pi -2 t)}=\frac{\log(2 t) (\pi t-(\pi -2 t) \tan t)}{2 t^2} $$ $$ S_5=-\sum _{k=-\infty }^{\infty } \frac{8 t \log(2 t)}{(\pi +2 k \pi )^2 (\pi +2 k \pi -2 t)}=\frac{\log(2 t) (t-\tan t)}{t} $$ Hence $$ I=S_1+S_2+S_3+S_4+S_5-\sum^{\infty}_{k=-\infty}\frac{4\log(\pi+2k\pi-2t)}{\pi^2(2k+1)^2}+C $$ Hence $$ \int^{\tan t}_{c}\frac{dx}{\arctan x}=\log(2t)+\frac{\tan t}{t}-\sum_{k\in\textbf{Z},k-odd}\frac{4\log(\pi k-2t)}{\pi^2 k^2}+C\textrm{, }0<t<\frac{\pi}{2}.\tag 3 $$ The logarithm is defined as $\log x:=\{\log x$, $x>0$ and $i\pi+\log(-x)$, when $x<0\}$.
$$ \int\frac{dx}{\arctan x}=\log\left(2\arctan x\right)+\frac{x}{\arctan x}- $$ $$ -4\sum^{+\infty}_{k=-\infty}\frac{\log\left(\pi (2k+1)-2\arctan x\right)}{\pi^2 (2k+1)^2}+C= $$ $$ =\log\left(2\arctan x\right)+\frac{x}{\arctan x} -4\sum^{+\infty}_{k=-\infty}\frac{\log(\left|\pi (2k+1)-2\arctan x\right|)}{\pi^2 (2k+1)^2}+C,\tag 4 $$ where $x>0$.

Notes.

This is the graph of $\int^{\tan t}_{\tan 1}\frac{1}{\arctan x}dx$ and the evaluation I found where the sum is trancated at $k=5$

At $t=e/2$ cutting the sum in $k=100$, we get

At $t=e/2$ cutting the sum in $k=1000$, we get

This is the graph's of $\int^{t}_{1}\frac{1}{\arctan(x)}dx$ and the evaluations and the evaluation (4):

Answer 3

Long Comment

Similar idea to @YuriNegometyanov:

$$I(x)=\int\limits_1^x \dfrac{\text dt}{\arctan t}=\int_{\tan ^{-1}(1)}^{\tan ^{-1}(x)} \frac{\tan ^2(u)+1}{u} \, du,\tag1$$

$$I(x)=\int_{\tan ^{-1}(1)}^{\tan ^{-1}(x)} \frac{1}{u} \, du+\int_{\tan ^{-1}(1)}^{\tan ^{-1}(x)} \frac{\tan ^2(u)}{u} \, du,\tag2$$

$$I(x)=\log \left(\frac{16 \tan ^{-1}(x)}{\pi^2 }\right)+x^2 \log \left(\tan ^{-1}(x)\right)-2\int_{\tan ^{-1}(1)}^{\tan ^{-1}(x)} \log (u) \tan (u) \sec ^2(u) \, du,\tag3$$

The integral in (3) can also be expressed in terms of the infinite series for $\tan u$, since

$$\frac{d^2 \tan (u)}{d u^2}=2\tan (u) \sec ^2(u)=2 \sum _{k=1}^{\infty } \frac{(2 k-2) (2 k-1) \left(\left(2^{2 k}-1\right) \zeta (2 k)\right) x^{2 k-3}}{\pi ^{2 k}}$$

and

$$\int x^{2 k-3} \log (x) \, dx=\frac{ (2 (k-1) \log (x)-1)}{4 (k-1)^2}x^{2 k-2}$$

Answer 4

This is not a complete answer either, but more observations. Consider

$$\int \frac{1}{\tan^{-1}(x)} dx$$

and substitute $x = \tan u$, so $dx = \sec^2 u\ du$. Then

$$\int \frac{1}{\tan^{-1}(x)} dx = \int \frac{\sec^2 u}{u}\ du$$

Now note that $\sec^2 u = 1 + \tan^2 u$ so we can write this as

$$\int \frac{\sec^2 u}{u} du = \int \frac{1}{u}\ du + \int \frac{\tan^2 u}{u}\ du = \ln u + \int \frac{\tan^2 u}{u}\ du$$

Hence, to have a form similar to the ones you've given for $\frac{1}{\sin^{-1}(x)}$ and the like, you'd need to have a new special function for either

$$\int \frac{\sec^2 u}{u}\ du$$

or

$$\int \frac{\tan^2 u}{u}\ du$$

I don't know if these can be solved in terms of

$$\int \frac{\sec u}{u}\ du$$

or

$$\int \frac{\tan u}{u}\ du$$

.

Answer 5

This addendum will be for extra ideas found. All answers are pretty much similar and are for fun. Graphical proof with root at 1.28… of @Nikos Bagis’s answer; note that desmos cannot be used to check the hyperbolic version of their answer as it has complex parts.

Note that C can be a complex number because of $\mathrm{ln(tan^{-1}(ix))=\frac{\pi i}{2}+ln(tanh^{-1}(x))}:$

1. $$\mathrm{Th(x)=\int\frac{dx}{tanh^{-1}(x)}=\int\frac{i\,dx}{tan^{-1}(ix)}=\int\frac{2dx}{ln(1+x)+ln(1-x)}=T(ix)=C+\frac{x}{tanh^{-1}(x)}+ln\left(tanh^{-1}(x)\right)+\frac12\sum_{n=2}^\infty \frac{4^n\left(4^n- 1\right) B_{2n}\left(tanh^{-1}(x)\right)^{2(n-1)}}{(n-1)(2n)!}=C+ \frac{x}{tanh^{-1}(x)}+ln\left(tanh^{-1}(x)\right)-\frac{4}{\pi^2}\sum_{n\in\Bbb Z}\frac{ln\left|\pi(2n+1)-2i\,tanh^{-1}(x)\right|}{(2n+1)^2}}$$

Specific values with expanded logarithms. A result verification and graph of Th(x) with root at x=$.3…$ and Result verification for last sum. For the graph, note the “i” parameter has to be infinity. Then, one takes a limit as x approaches 1 of the evaluation limits for the sum. This has to be done if an integral bound is 1 as the inverse hyperbolic tangent of 1 is 0 and approaches infinity as a result of the reciprocal and improper integral.

2.$$\mathrm{\int_\frac1{\sqrt{3}}^1\frac{dx}{tan^{-1}(x)}= T\left(\frac1{\sqrt3}\right)-T(1)=\frac{4-2\sqrt3}\pi+ln(3)-\ln(2)-\frac1{2\pi^2}\sum_{n=2}^\infty \frac{B_{2n}(-4)^n \pi^{2n}\left(4^n-1\right)\left(4^{2-2n}-6^{2-2n}\right)}{(n-1)(2n)!}= \frac{4-2\sqrt3}\pi+ln(3)-\ln(2)-\frac{4}{\pi^2}\sum_{n\in\Bbb Z}\frac{ln\left|1-\frac{1}{4(3n+1)} \right|}{(2n+1)^2}=.6457455…}$$

3.$$\mathrm{\int_{1-\frac{2}{e+1}}^\frac12 \frac{dx}{tanh^{-1}(x)}=Th\left(1-\frac{2}{e+1}\right)-Th\left(\frac12\right)=\frac{4}{e+1}-\frac1{ln(3)}+ln(ln(3))-2+2\sum_{n=2}^\infty\frac{B_{2n}4^n\left(4^n-1\right)\left(ln^{2n-2}(3)-1\right)}{2^{2n}(n-1)(2n)!}=.0722855…}$$

The other sum representation using @Nikos’s method evaluates to a different constant even with small modifications:

$$\mathrm{ \frac{4}{e+1}-\frac1{ln(3)}+ln(ln(3))-2-\frac{4}{\pi^2}\sum_{n\in\Bbb Z}\frac{ln\left|\frac{\pi(2n+1)-i}{\pi(2n+1)-i\, ln(3)}\right|}{(2n+1)^2}\mathop=^{??} .0722855…}$$

Please correct me and give me feedback!

I wonder what would happen if we expanded and separated the sums…