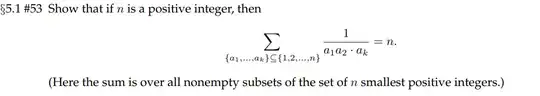0

Discrete Mathematics and Its Applications, 7th edition, Global Edition, Kenneth Rosen, Kamala Krithivasan is the textbook I am referencing here.

I came across this problem. problem encountered

I am trying to learn how to do mathematical induction.
However, I can't help but be confused at how I would go about with substituting in P(k) and P(k+1) so that I can prove these are equal to n?

Like how would that work out to if k and k+1 are subbed in and how do I go about with simplifying the P(k+1) expression such that it proves that P(k+1) holds?

$$P(k): \ \ \ \ \sum _{\{a_1,...,a_i\}\subset\{1,2,...,k\}}\dfrac{1}{a_1.a_2...a_i}=k \tag{1}$$

I have proven that P(1) is true as 1 ⊆ 1, in summation is 1 which is n. So P(1) holds.

Not sure how I should go about with finding/proving P(k) and P(k+1) and how would it look in working?

Any help is appreciated, thank you! :)

Jean Marie
  • 88,997
Megan Darcy
  • 139
  • Look at the way I have edited formula called (1): I think you were "fooled" by the fact that your index called $k$ isn't the $k$ of the recurrence property : it is why I have changed the former $k$ into $i$ and the former $n$ into $k$ (at two places). Is it clearer now ? – Jean Marie Jul 06 '21 at 14:24
  • yup! you're right I was confused by the meaning of k in the original version. So the edited version makes alot more sense and looks familiar. thanks! @JeanMarie – Megan Darcy Jul 06 '21 at 17:04

2 Answers2

2

Hint

When you move from $k$ to $k+1$ the RHS will be $k+1$ while the sum on the LHS will have all the summands for the case $k$ plus $k+1$ new summands that amounts to the $k$ previous summand multiplied by $\dfrac {1}{k+1}$ and the last one: $\dfrac {1}{(k+1)}$.

Putting all together, the LHS will be: $k+k \dfrac {1}{(k+1)} + \dfrac {1}{(k+1)}$.

The idea is to list all subsets: with $\{ 1,2,\ldots, k \}$ they are $2^k$ and the non-empty ones are $2^k-1$.

In the induction step we move from $k$ to $k+1$ and we have the new "base set" $\{ 1,2,\ldots, k, k+1 \}$. The non-empty subsets are now $2^{k+1}-1=(2^k\times 2)-1=(2^k-1)\times 2 +1$.

How we get them? using all the previous subsets ($2^k-1$) plus all the new ones obtained from the previous ones adding the each of them the new element $k+1$ (and thus $2^k-1$ new elements) and the new subset $\{ k+1 \}$ (the "last" one).

Mauro ALLEGRANZA
  • 99,247
  • hi! sorry could you explain why there is a "last one" of 1/(k+1) ? where does it come from? thanks :) – Megan Darcy Jul 06 '21 at 17:03
  • So that means that from P(k), RHS = k originally consists of the summation of each subset, the subsets with each other and all the subsets summed? So that's how you got the k(1/(k+1)) element as well? – Megan Darcy Jul 06 '21 at 17:22
1

  1. Compare the way I have edited formula that I have called (1) with the formula above as given in the book: I think you were "fooled" by the fact that your index called k isn't the k of the recurrence property: it is why I have changed the former k into i and the former n into k (at two places).

  2. Dealing with the proof itself, a key fact is that the summation on the LHS of (1) can be transformed into a product (See this question and its answers):

$$\left(1+\frac{1}{1}\right)\left(1+\frac{1}{2}\right)...\left(1+\frac{1}{k}\right)$$

making the recurrence step : $P(k) \to P(k+1)$ very easy.

See as well here.

A cousin interesting issue can be found [here] (A summation involving the inverses of the products of the elements of subsets of a set).

Jean Marie
  • 88,997