5

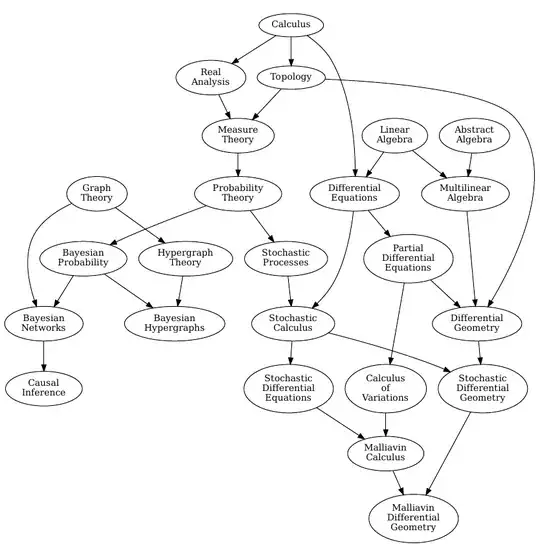
I've constructed a directed acyclic graph that leads from introductory subjects, such as calculus (single and multivariable) to some of my current interests including causal inference, Bayesian hypergraphs, and Malliavin differential geometry. The arcs indicate that something in one subject is required by another, with some relaxation in noting that there is transitivity across the graph. I've excluded set theory as too obvious and universal, and hypernetworks and simplicial complexes as merely borderline to my interests as of this moment.

enter image description here

You can produce the diagram for yourself with the following code which is provided below.

from graphviz import Digraph

g = Digraph()


Calculus


g.edge('Calculus', 'Real\nAnalysis')
g.edge('Calculus', 'Topology')
g.edge('Calculus', 'Differential\nEquations')


Linear Algebra


g.edge('Linear\nAlgebra', 'Differential\nEquations')
g.edge('Linear\nAlgebra', 'Multilinear\nAlgebra')


Abstract Algebra


g.edge('Abstract\nAlgebra', 'Multilinear\nAlgebra')


Real Analysis


g.edge('Real\nAnalysis', 'Measure\nTheory')


Topology


g.edge('Topology', 'Measure\nTheory')


Measure Theory


g.edge('Measure\nTheory', 'Probability\nTheory')


Probability Theory


g.edge('Probability\nTheory', 'Bayesian\nProbability')
g.edge('Probability\nTheory', 'Stochastic\nProcesses')


Bayesian Probability


g.edge('Bayesian\nProbability', 'Bayesian\nNetworks')


Graph Theory


g.edge('Graph\nTheory', 'Bayesian\nNetworks')
g.edge('Graph\nTheory', 'Hypergraph\nTheory')
g.edge('Bayesian\nProbability', 'Bayesian\nHypergraphs')


Hypergraph Theory


g.edge('Hypergraph\nTheory', 'Bayesian\nHypergraphs')


Bayesian Networks


g.edge('Bayesian\nNetworks', 'Causal\nInference')


Stochastic Processes


g.edge('Stochastic\nProcesses', 'Stochastic\nCalculus')


Differential Equations


g.edge('Differential\nEquations', 'Partial\nDifferential\nEquations')
g.edge('Differential\nEquations', 'Stochastic\nCalculus')


Partial Differential Equations


g.edge('Partial\nDifferential\nEquations', 'Calculus\nof\nVariations')
g.edge('Partial\nDifferential\nEquations', 'Differential\nGeometry')


Stochastic Calculus


g.edge('Stochastic\nCalculus', 'Stochastic\nDifferential\nEquations')
g.edge('Stochastic\nCalculus', 'Stochastic\nDifferential\nGeometry')


Stochastic Differential Equations


g.edge('Stochastic\nDifferential\nEquations', 'Malliavin\nCalculus')


Calculus of Variations


g.edge('Calculus\nof\nVariations', 'Malliavin\nCalculus')


Topology


g.edge('Topology', 'Differential\nGeometry')


Multilinear Algebra


g.edge('Multilinear\nAlgebra', 'Differential\nGeometry')


Differential Geometry


g.edge('Differential\nGeometry', 'Stochastic\nDifferential\nGeometry')


Malliavin Calculus


g.edge('Malliavin\nCalculus', 'Malliavin\nDifferential\nGeometry')


Stochastic Differential Geometry


g.edge('Stochastic\nDifferential\nGeometry','Malliavin\nDifferential\nGeometry')


g.view()

What I would like to know is if there are any subjects that I have left out. You're welcome to comment on other flaws in the DAG, and feel free to use the code to show me how you think it 'should' be structured in your answer, but I am primarily interested in missing subjects.

Galen
  • 1,946
  • Hey, I have a few questions. (1) What do you mean by Malliavin Differential Geometry? ; (2) What is the primary purpose of this illustration? I'm sure the topics are connected to each other but you often only need very little background knowledge from the previous topics. – Mundane_Matters Jul 18 '21 at 06:32
  • I should add, if you are trying to learn Malliavin Calculus or some topics in the Probability Theory side, I have found a reasonable compromise of background information needed and books I found particularly useful that I can share with you. – Mundane_Matters Jul 18 '21 at 18:30
  • @Mundane_Matters (1) Doing Malliavin calculus on differentiable manifolds; (2) Shows a rough outline of the conceptual requires. I agree that some of these topics require relatively little background. – Galen Jul 19 '21 at 14:15
  • @Mundane_Matters I would appreciate any resources on Malliavin calculus. – Galen Jul 19 '21 at 14:17
  • Can you tell me what your background in mathematics is like? And, what is your purpose for learning Malliavin Calculus? – Mundane_Matters Jul 20 '21 at 00:12
  • @Mundane_Matters You can definitely throw abstractions at me, even up to universal algebra and category theory if need be. Not that I am expect those topics here, but I state them as the least upper bound of what I would knowingly approach. But I am a computational scientist, so I am also quite happy to see Monte Carlo methods, Runge-Kutta, and parameter tuning. Malliavin calculus has the appeal of modelling (1) dynamics, (2) stochasticity, and (3) transformational invariance in a single system. – Galen Jul 20 '21 at 00:39
  • @Mundane_Matters Looks like we have similar interests. – Galen Jul 20 '21 at 00:42
  • 1
    “Galen is a science and technology enthusiast dedicated to life-long learning.” - We definitely do :)

    I wish I knew more appropriate resources. However, if your purpose is to learn Malliavin Calculus you can’t go wrong with Nualart’s “The Malliavin Calculus and Related Topics”. I would read it together with Kunze’s lecture notes (which can be found online via google) which very strongly follow parts of the first two chapters of Nualart. Kunze adds more preliminary knowledge which Nualart takes for granted. Kunze is also occasionally more explanatory in his proofs.

     – Mundane_Matters Jul 20 '21 at 02:03
  • 1
    Nualart took a little getting used to for me as he often likes to skip parts in the proofs (maybe intentionally for the reader) so I would make sure I work out everything myself.

    Now, to get through most of Nualart, you’d need Stochastic Calculus (at the level of Le Gall) and some Functional Analysis (Any one of the popular references is sufficient, I personally just read Folland and wikipediad/googled the rest throughout my journey).

     – Mundane_Matters Jul 20 '21 at 02:04
  • 1
    Some PDE and Distribution Theory knowledge would be useful for a more complete understanding, but you can get by with googling the information as it comes and taking some of the theorems for granted.

    Another book I would recommend is “Differentiable Measures and the Malliavin Calculus” by Vladimir I. Bogachev which assumes more or less the same background and takes a different but equally interesting approach. Both have exercises as well.

     – Mundane_Matters Jul 20 '21 at 02:04

1 Answers1

1

Connection between Linear Algebra and Graph Theory

I think some form of connection between graph theory and linear algebra would make a lot of sense. Much of graph theory analyzes graph adjacency matrices with all kinds of tools from linear algebra. This connection extends to causal inference, where ideas from linear algebra are often used to learn or analyze causal structures. For example, the adjacency matrix $A \in \mathbb{R}^{d\times d}$ of any directed acyclic graph (DAG) can be reordered to be upper triangular, meaning that it is invertible, and that $\mathrm{tr}(e^A) = d$, etc.

Scriddie
  • 236