4

I am looking for "beautiful" arrangements of $k$-ary necklaces of length $ak$ where each of the $k$ types of bead appears $a$ times ($a \geq 1$ a natural number).

A necklace is considered beautiful if the sequence of gap lengths for all $k$ types of bead are equivalent under rotation. A gap length is the number of beads between one bead of a given type and the next bead of that type in the necklace. The sequence is formed by taking the gap lengths between pairs of beads of that type going, say, clockwise.

A trivial solution is to define the sequence of gap lengths as $(k-1,\ldots,k-1)$, where a beautiful necklace arranged per this trivial solution could then be $(1,\ldots,k,\ldots,1,\ldots,k)$. Another trivial solution is to define the sequence of gap lengths as $(0,\ldots,0,a(k-1))$, where a beautiful necklace arranged per this trivial solution could then be $(1,\ldots,1,2,\ldots,2,\ldots,k,\ldots,k)$. We'll call other solutions non-trivial.

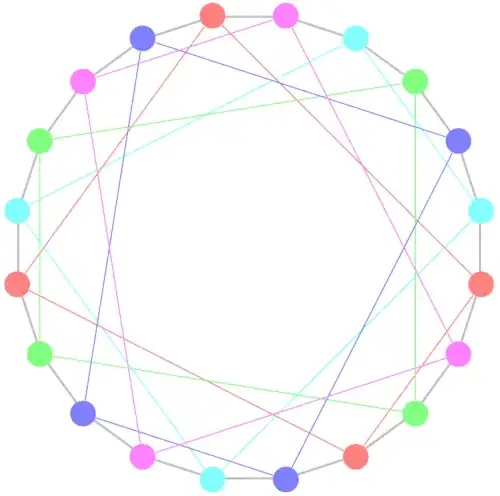
There appear to be non-trivial solutions, at least for some values of $a$ and $k$. Here's a quick (and slightly dirty) illustration of one for $k=5$, $a=4$, with gaps $(2,5,4,5)$. To help see the rotational symmetry of the gaps, I've added edges to connect the pairs of nearest beads of the same type.

enter image description here

All I can say right now is (trivially) that the gap lengths must sum to $a(k-1)$ for each type. I suspect some relation of the gap lengths to the factors of $ak$, but I am not certain.

Given particular values for $a$ and $k$, how can I find beautiful arrangements of necklaces with non-trivial solutions? Or what can I say about the gaps in such arrangements?

badroit
  • 826

1 Answers1

3

Your example is an instance of a general family of solutions: Start by placing the beads in the trivial pattern $$ 1,1,\ldots, 1, 2, \ldots 2, \ldots, k, \ldots k $$ Then split the necklace into $a$ regular $k$-gons (each of them with one bead of each color), and rotate the colors of each $k$-gon by an arbitrary number of steps.

In your example the four regular pentagons have been rotated by $0$, $2$, $3$, and $0$ positions.

In general, if you rotate the $k$-gon formed of the last bead in each color run one step away from its companions, you get a non-trivial solution unless $a=1$ or $k\le 2$ or $(a, k)$ is $(2,3)$.

There are also non-trivial solutions of this shape for $k=2, a\ge 4$: $$ 2, \underbrace{1, \ldots ,1}_{\text{all }1}, 2, 1, \underbrace{2, \ldots 2}_{\text{all }2}, 1 $$

This method does not make gap lengths simple to read off from the rotation amounts from each of the $k$-gons, though.

Not all solutions have this form, though -- in particular, there are solutions where the rotations that takes one color to another is not always a multiple of $a$. In particular, this is the case for the trivial $(1,\ldots, k, \ldots, 1,\ldots k)$ solution if $a$ and $k$ have a common prime factor. Another is, for example $$ 1,2,1,2,1,2,3,4,3,4,3,4,5,6,5,6,5,6 $$ So this is not a complete classification of all solutions.

Note, by the way, that the gap lengths alone do not determine the shape of the necklace. For example, $(a,k)=(2,6)$ with gap lengths $2,8$ can be realized as either $$ 1,2,3,1,2,3,4,5,6,4,5,6 $$ or $$ 1,6,2,1,3,2,4,3,5,4,6,5 $$

Troposphere
  • 7,637