$$\begin{align}x&=tx′−(x′)^3\\x(3)&=−2\end{align}$$
This is how I tried.
put $x' = p$
$x = tp - p^3$
then differentiate
$p = p + tp' - 3p^2p'$
$0 = (t-3p^2)p'$.
if $p' = 0 , p = C$ ...
but I couldn't make it.
Can you help me with explanation and answer?
+1, for the good attempt shown and also, you are almost there.
This is an example of the Clairuat Equation.
The Clairaut ODE looks like $$y = xy' + f(y')$$ and it is solved exactly in the manner you have solved.
It results in two solutions:
You can use this to find the final answers.
That's an interesting problem, in fact there are three local solutions! $$ x(t) = 1-t;$$ $$ x(t) = 2t-8;$$ $$ x(t) = -\frac{2t\sqrt t}{3\sqrt 3}.$$ We may check by direct substitution that all these three functions solve the problem. By the way they correspond to the "three" initial values for the first derivative $x'(3)=p_0$: $$3p_0 - p_0^3= x(3) = -2$$ $$\leftrightarrow \quad (p_0 +1)^2 (p_0-2) = 0$$ $$\leftrightarrow \quad x'(3) = -1 \quad \text{or}\quad x'(3) = 2,$$ where $x'(3)=-1$ counts "double".
Here is a picture of the three algebraic curves that contain the three local solutions:
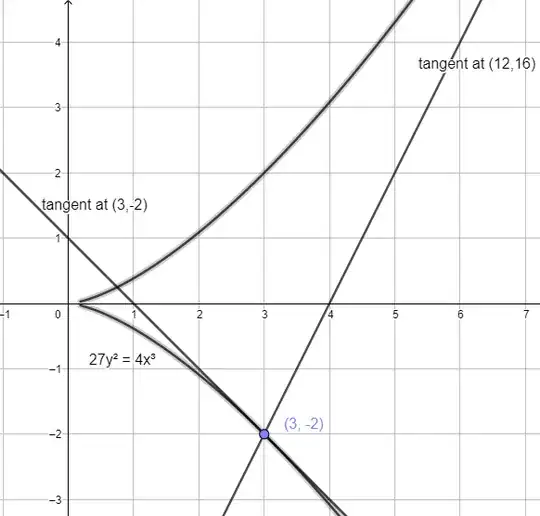$y=1-x$, $y=2x-8$ and $y^2 = \frac{4x^3}{27}$. " />
Clairaut says that there are infinitely many global solutions
Beware, these three formulae tell us only the local form of the solutions. If we want global solutions, there are actually infinitely many solutions. For example, here is one:
$$x(t) =\begin{cases} -\frac{2t\sqrt t}{3\sqrt 3} & t<300; \\ -10t+1000 & t\geq 300.\end{cases}$$ How to find all possible trajectories? Long story short: monsieur Alexis Clairaut published in 1734 a method to solve this type of differential equations (and you came very close to find it and apply it in this particular case):
Clairaut, Alexis Claude (1734), "Solution de plusieurs problèmes où il s'agit de trouver des Courbes dont la propriété consiste dans une certaine relation entre leurs branches, exprimée par une Équation donnée.", Histoire de l'Académie royale des sciences: 196–215.)
I will apply the method to your problem and find all the trajectories where all segments of solutions can lie. In the previous displayed formula I gave an example of a solution that is composed of a nonlinear segment valid up to $t=300$ and that then continues, at $t\geq 300$, on another, linear, trajectory.
This is a Clairaut's equation
This is an example of a Clairaut's equation, which more generally is a differential equation of the form
$$x = t x' + f(x'),$$
where $f$ denotes a continuously differentiable function. Here $f(z)=-z^3$.
To solve, first you differentiate once
Clairaut's equations are usually solved exactly with your approach! When you differentiate you first get $x'= x'+tx'' + f(x')x''$. Then the term $x'$ disappears and we are left with
$$0=(t+f'(x'))x'' $$
exactly like you already noticed. Here $f'(z)=-3z^2$.
There are two types of solutions. The general solution is a linear function
Now I tell you how to continue. The main thing to note is that at every point we either have $$x''=0 \quad \text{or}\quad t+f'(x')=0.$$ When $x''=0$ then we speak of a general solution to the Clairaut's equation. If a function $x(t)$ satisfies $x''=0$, then it must be of the form $$x(t) = a t + b$$ for some $a,b$. If you put this formula into the original equation, we get $at+b=at+f(a)$ and so $b=f(a)$. In other words, the general solution has the form $$x(t)= at + f(a),$$ where $a$ is some arbitrary parameter. In your case these are $x(t)=at-a^3$. Here is a plot of these lines for $-1\leq a\leq 9$.
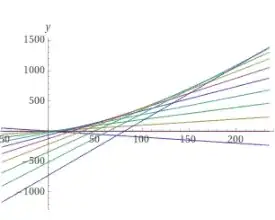$x(t)=at-a^3$ for $-1\leq a\leq 9$." />
The singular solution is an envelope of the lines of the general solution
There is one more solution, which is called the "singular solution" of the Clairaut's equation. This corresponds to the case
$$ t+f'(x')=0.$$
In your case, you need to solve $t-3(x')^2=0$. So:
$$x'(t) = \pm\sqrt {t/3}.$$
Now I will take the "+" sign. The "-" sign is similar. To find $x(t)$ we can for instance just integrate:
$$x(t) = \int \sqrt{t/3} = \frac 2 {3\sqrt 3} t^{3/2}+C$$
and to find $C$ we use the original equation. If we put this formula in the original equation we get
$$ \frac 2 {3\sqrt 3} t^{3/2}+C = \frac 1 {\sqrt 3} t^{3/2} - \frac 1 {3\sqrt 3} t^{3/2},$$
so $C=0$. Here is the plot of
$$x(t) = \frac 2 {3\sqrt 3} t^{3/2}.$$
Note that its graph is an envelope of the lines found in the "general solution" part!
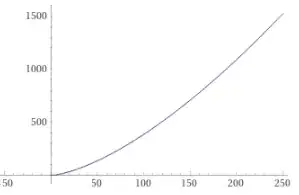$x(t) = \frac 2 {3\sqrt 3} t^{3/2}$." />
