Give a non-linear ( if it helps, multi-linear ) system for the variable with $\mathbf{Z} = [\mathbf X_1, \ldots, \mathbf{X_n} ]^T$: $$ \dot{\mathbf{Z}} = F ( \mathbf{Z}, \mathbf{u} ) $$ and an unknown equilibrium point $\mathbf{Z^*}$ (i.e. 0 = F ($\mathbf{Z^*})$ ).
Is there any known way to design such a control $\mathbf{u^*}$ for which:
?
Thanks in advance.
Yes this is possible (for some systems). You can take a look at:
Bazanella, Alexandre S., Petar V. Kokotovic, and Aguinaldo S. e Silva. "On the control of dynamic systems with unknown operating point." 1997 European Control Conference (ECC). IEEE, 1997.
In short, if you have a system:
$$ \dot{x}=f(x)+g(x)u $$
and $f(x^*) = 0$ but you don't know $x^*$ then you can use $u=\varphi(x-x^*)$ together with an adaptive control loop that estimates $x^*$:
$$ \begin{align} \dot{x} &= f(x)+g(x)\varphi(x-\theta)\\ \dot{\theta}&=A(x-\theta) \end{align} $$
In the paper you can find some ideas how you can find $A$.
They also have this example:
$$ \dot{x} = \sin(x) - \frac{1}{2}+u $$
Assume you don't know that one equilibrium is $x^*=\frac{\pi}{6} = 30°$. So:
$$ \begin{align} \dot{x} &= \sin(x) - \frac{1}{2}+u\\ u&=-k(x-\theta)\\ \dot{\theta}&=a(x-\theta) \end{align} $$
I use higher gains than in the paper: $k=150,a=-100$. Simulation with $x(0)=0,\theta(0)=0$:
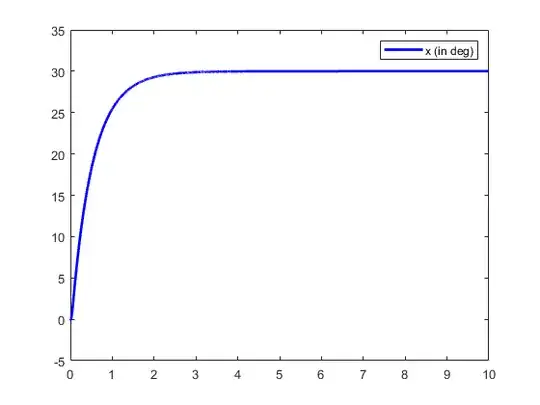
You can see the controller stabilizes the unknown operating point at $x=30°$ without having any knowledge about that point.
