My problem is this:
Given a necklace with length $N$, how many ways to color it using $2$ colors, such that any rotation should be counted only once?
For example, following $2$ necklaces should only be counted once.
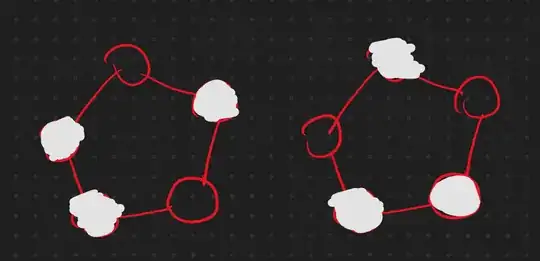
What I tried was to reduce problem into something different, which is for every number $K | 1\leq K \leq N$, K is the number of black painted nodes. (I will call them nodes, also will use black-white as colors.).
We can think the place between every adjacent pair of black nodes as a box, and think every edge as a bead.
With this idea, the problem reduces to;
How many ways to put $N$ beads into $K$ boxes such that every box have at least one bead?
That can be calculated with the given formula: $\binom{N - 1}{K - 1}$
For example, we can show the necklaces on the top of this post as, $2 - 2 - 1$. We can see that every permutation of $2 - 2 - 1$ is actually representing the same necklace. So I'll instead use another example of $K = 4$ colors with $N = 11$. Let's just say $3 - 5 - 2 - 1$, well we can see that for example $5 - 2 - 1 - 3$ is still the same necklace. But $2 - 5 - 1 - 3$ is not the same necklace. I don't know how to calculate without this duplicates.
I actually tried to derive something, that:
$5 - 1 - 2 - 3$
$3 - 5 - 1 - 2$
$2 - 3 - 5 - 1$
$1 - 2 - 3 - 5$
With the power of guessing, I tried $\sum_{K = 1}^{N - 1}\frac{\binom{N - 1}{K - 1}}{K + 1}$, for $N = 11$, it results with $186 + 1$(all of the nodes are white -> $K = 0$) $+$ $1$(all of the nodes are black -> $K = N$)
Edit: Small correction, (K + 1) on the above formula should be (K) instead. That is $\sum_{K = 1}^{N - 1}\frac{\binom{N - 1}{K - 1}}{K}$, which simpflies to $\frac{2^N - 2}{N}$ and works only when $N$ is prime. Also don't forget to add $2$ because of $K = 0$ and $K = N$.
$= 188$, and according to my book, it's correct. But since I don't have any proof or anything, I don't know if it's correct or not.
Though, for $N = 9$, according to the book, answer is $60$. But the formula gives $56.6$, with the +2, it's $= 58.6$. So I guess I'm still missing a point.
Thank you for your answers in advance.