The actual answer of this is e^-8 .But why do i get the answer as 1 when i evaluate the following limit like this -
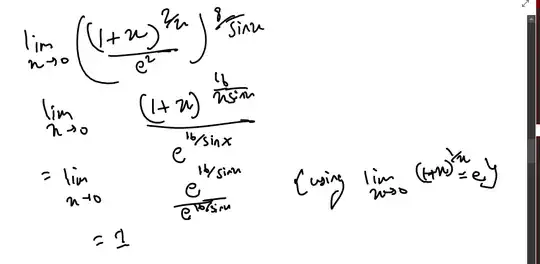
- 501
-
8Please use MathJax instead of images with formulas. For some basic information about writing mathematics at this site see, e.g., basic help on mathjax notation, mathjax tutorial and quick reference, main meta site math tutorial and equation editing how-to. – md2perpe Jun 13 '21 at 20:53
-
Please pay regard to limit laws. Just as you can't write $\sqrt {a+b} =\sqrt{a} +\sqrt{b} $ you can't move from second expression to third expression. That's an invalid step. The meaning of $\lim_{x\to 0}(1+x)^{1/x}=e$ is that you can replace $\lim_{x\to 0}(1+x)^{1/x}$ with $e$ but it does not mean that you can replace $(1+x)^{1/x}$ with $e$ during limit evaluation as $x\to 0$. – Paramanand Singh Aug 27 '21 at 10:06
-
See more details in this answer. – Paramanand Singh Aug 27 '21 at 10:09
-
@ParamanandSingh sir , thanks for this , Ill come back soon with some counter examples – Raghav Madan Aug 27 '21 at 22:23
-
currently downvoting since no latex/mathjax/mathsjax – BCLC Aug 30 '21 at 23:38
-
1"I want some proper answers" this will need some clarification, and I need to understand your work. I'd also like to know what zhw's answer lacks, because to me it explains your error for sure : it's a recent answer which seems to give what you ask for. Having said that, do try to write in MathJax in the future (Note : I had to write in MathJax because my handwriting is , by a diameter of the sun traversed a myriad times, much worse than yours). – Sarvesh Ravichandran Iyer Aug 31 '21 at 12:51
-
@TeresaLisbon ok thanks for advice .Which country are you from, ? – Raghav Madan Sep 09 '21 at 13:54
-
@RaghavMadan India. – Sarvesh Ravichandran Iyer Sep 09 '21 at 15:25
-
@TeresaLisbon ohh , from your name it didn't seem like you are from any asian country . Is it your real name ? if not then whats it – Raghav Madan Sep 09 '21 at 17:08
-
@RaghavMadan Real name is , on my profile page. It's written in an Indian language (yes, my name is actually that long, in case you just saw it!). Putting that through a translator gets one Kalyanasundaram Srinivasan Krishnamurthy Ravichandran Iyer, which is basically my identity, for all practical purposes! – Sarvesh Ravichandran Iyer Sep 09 '21 at 17:11
-
@RaghavMadan No , thankfully not! I'll be difficult to find apart from MSE : yes I do have a mail account, but it's a near official account and MSE is not official work for me. Therefore, I use only MSE to interact about MSE related matters. In particular I will respond if you ping me somewhere, for sure. – Sarvesh Ravichandran Iyer Sep 09 '21 at 17:23
4 Answers
Your proof is wrong in going from line 2 to line 3. You say you are just using the "algebra of limits" there, but that is not true.
The algebra of limits says if $f,g$ have limits $L,M$ at $a,$ then $\lim_{x\to a}(f(x)+g(x)) = L+M,$ $\lim_{x\to a}(f(x)g(x)) =LM,$ etc. Which of these basic results allows us to go from line 2 to line 3?
Here's something to consider: Line 2, after some simplifying, is
$$\tag 1 \left (\frac{(1+u)^{1/u}}{e}\right )^{16/\sin u}.$$
As you may recall, $(1+u)^{1/u}/e<1$ for small positive $u.$ And $16/\sin u$ is huge for small positive $u.$ So we're taking something in $(0,1)$ and raising it to a very large power. It's not surprising that the answer turns out to be a number less than $1.$
On to the desired limit: It's good to recall logarithms are wonderful things in this kind of context. So apply $\ln$ to $(1)$ to get
$$\frac{16}{\sin u}\left (\frac{1}{u}\ln (1+u)-1\right ).$$
Now Taylor tells us $\ln(1+u)=u-u^2/2 +O(u^3)$ as $u\to 0.$ A little bit of work then shows the above equals
$$\frac{1}{\sin u}\left (-8u + O(u^2)\right )=-8\frac{u}{\sin u} + \frac{O(u^2)}{\sin u}.$$
The limit of this as $u\to 0$ is $-8\cdot 1+0=-8.$ Exponentiating back gives $e^{-8}$ for the desired limit.
- 107,943
When you take a limit of an expression, you can't take the limit of just a part of the expression (such as the numerator) and leave the rest of the expression the same. That seems to be what you did in the third line.
To see why this is wrong, just consider this example: $$\lim_{x \to 0}\frac{x}{x}$$ If I just take the limit in the numerator only, I get $$\lim_{x\to 0} \frac{0}{x}$$ Obviously these are not equal - the first one is 1 and the second is 0.
- 35,732
-
No basically the second one is not lim x->0 0/x. It is lim x->0 (->0/x) .What i did while evaluating the limit was just applying algebra of limits – Raghav Madan Jun 13 '21 at 20:52
-
2The algebra of limits requires that you take all limits simultaneously. That is not what you did. You took a limit of part of the expression in the numerator and left everything else the same. That's the same error as what I showed above in a simplified way. – Ted Jun 13 '21 at 20:53
-
Doesn't the algebra of limits in the case of a quotient assume the limit of the denominator is not $0?$ – zhw. Aug 30 '21 at 23:23
You made a mistake when you wrote that
$$(1+x)^{\frac{16}{x\sin(x)}}=$$
$$e^{\frac{16}{x\sin(x)}\ln(1+x)}\sim e^{\frac{16}{\sin(x)}}$$
because $\ln(1+x)\sim x$.
In fact we have
$$e^{f(x)}\sim e^{g(x)}\iff \lim (f(x)-g(x))=0$$
- 63,719
The expression whose limit you want to calculate is:
$\lim_{n\to 0}\Big(\frac{(1+n)^{2/n}}{e^{2}}\Big)^{\frac{8}{sin(n)}}$.
$\lim_{n\to 0}\Big(e^{\frac{-1}{sin(n)}}(n+1)^{\frac{1}{n.sin(n)}}\Big)^{16}$,
$=(e^{-1/2)})^{16}=e^{-8}$
- 1,781