0

How many squares of side length $x$ can fit in a circle of diameter $n\cdot x$, where $n$ is any positive number, such that none of the squares overlap the perimeter of the circle and all of the squares are aligned in a grid (i.e. no zig-zagging of edges)?

For example: 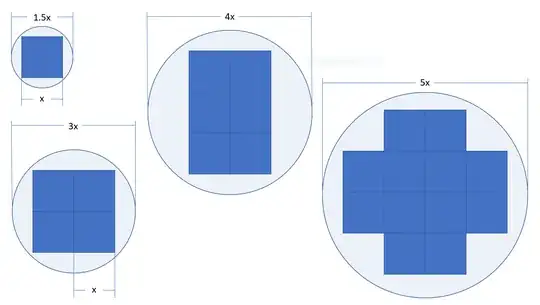enter image description here This is for a project I'm doing using Excel, so it'd be ideal to have a formula, versus an infinite series or a c++ function.

Thanks!

[Edit]: Some folks have suggested this solution but I think that only works when the circle is very large (relative to the squares). For example, a circle of 3x gives a result of 0.4, when clearly (from the image above) you can fit 4 squares inside.

RobPratt
  • 50,938
Stephen
  • 1
  • 5
    Does this answer your question? How many squares fit in a circle? If you search the web for square packing in a circle you will find several links that might be useful. – Ethan Bolker Jun 06 '21 at 18:51
  • Welcome to MSE! I don't know of any exact formulas, but for large $n$ the answer will be $\approx \frac{\pi}{4} n^2$, and the approximation gets better and better for larger and larger $n$. Indeed we're really approximating the area of a circle of radius $\frac{nx}{2}$ by squares of width $x$, and so the number needed will be roughly the ratio of their areas. – Chris Grossack Jun 06 '21 at 18:51
  • Even if you want the squares aligned in a grid, you can fit 7 squares into the circle with diameter $4x$, by moving your rectangle a bit left and adding another square to the middle right of the rectangle. – Misha Lavrov Jun 06 '21 at 19:45
  • See Misha's suggestion and may be we could be even more aggressive. Any limitation on square positions? – Moti Jun 07 '21 at 18:23

0 Answers0