10

Consider a equilateral triangle of total area 1. Suppose 7 points are chosen inside. Show that some 3 points form a triangle of area $\leq\frac 14$.

achille hui
  • 125,323
andrew
  • 143
  • 1
  • 5

3 Answers3

3

Choose one point $p$ and draw a line from $p$ to each of the other six points.

We can order the six points $a,b,c,d,e,f$ going clockwise around point $p$ and draw lines from $a$ to $b$, from $b$ to $c$, from $c$ to $d$, from $d$ to $e$ and from $e$ to $f$.

This gives five disjoint triangles which fit inside the triangle of area $1$.

Therefore the total area of the five triangles is less than or equal to one and at least one triangle has area less than or equal to $\frac 15$.

Tim
  • 5,744
  • Thank you very much. Could you explain why you say that "Therefore the total area of the five triangles is less than or equal to one and at least one triangle has area less than or equal to 1/ 5 " I don't exactly understand how you come up with 1/5 – andrew Jun 09 '13 at 21:25
  • @andrew: It probably helps if you draw an example. The 5 triangles together form an irregular heptagon that sits inside your triangle. The area of this heptagon is less than one. Now suppose $A$ is the area of the smallest of the five triangles. As the area of the heptagon is the sum of the areas of the five triangles we must have $1\geq 5A$ therefore $A\leq\frac 15$. – Tim Jun 10 '13 at 09:00
-1

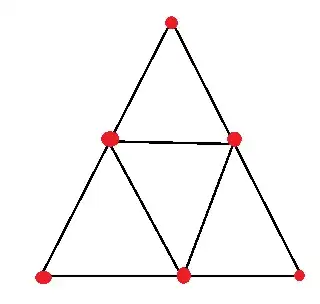
enter image description here

Divide the triangle into 4 equal size areas. As the diagram above, there are only 6 vertices the 4 triangles share such that the area of each group of 3 vertices is $\frac{1}{4}$, with any additional vertex attached will it fall into the center of any group of 3 vertices. Hence if 7 points are chosen, we can always see the area of 3 of them is less than $\frac{1}{4}$.

OOD Waterball
  • 195
  • 1
    I'd like you to clarify parts of the proof, please (it's an honest question, I teach this stuff at the moment to future math teachers). When you say "divide the triangle into $4$ equal size areas", do you mean "as shown above" or any subdivision? For example, I could come up with subdivision that uses only $5$ vertices. Now, if you fix this particular subdivision, what if I choose $7$ points such that all lie in the interiors of your $4$ triangles and no three points lie in the same triangle? I know how I'd finish that myself, but it's more involved. Am I missing something obvious? – Ennar Oct 24 '18 at 10:50
  • 1
    My point is that I'm not happy with this proof, but I really want it to work because it's very intuitive and easy to show to anyone. I used the same argument when I was in high school, but am not convinced in it anymore. – Ennar Oct 24 '18 at 10:54
-2

I have seen answers with 9 points (in comment link above) and 5 points (above).

However, not with 7 points. Please see below:

Drawlines from midpoints of all 3 sides to each other

Now we have 6 points (3 vertices and 3 mid points)

we have 4 triangles of equal area 1/4. (equilateral triangle)

To add the 7th point will create a triangle of area less than 1/4.

QED

New Student
  • 407