calculate $\int_{0}^{\infty} e^{-t^{2}} \sin \left(t^{2}\right) d t$ by residue theorem

Question

I am trying to calculate $\int_{0}^{\infty} e^{-t^{2}} \sin \left(t^{2}\right) d t$ by residue theorem, what I did according to the hint I got is take a path as follow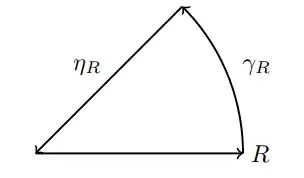

while it has angle $\theta = \frac{\pi}{8}$ and it go from the origin to $R$ like $[0,R]$ I showed that $\int_{[\eta_R]} f(z)= -e^{- \pi i/8} \int_{[0,R]} f(z) $ and now I just need take the limit $R \rightarrow \infty$ and calculate $\int_{[\gamma_R]} f(z)$ wich is a bit problem because I dont see any poles of that function, but this integral is nonezero.

Not quite a duplicate of https://math.stackexchange.com/questions/455882/integral-of-e-x2-cosx2-using-residues but close enough that the solutions there may shed light on this problem. — leslie townes, May 29 '21 at 15:06
In particular, your result that the integral on $\nu_R$ is $-e^{-i\pi/8}$ times the first integral is wrong. — Thomas Andrews, May 29 '21 at 15:15
@ThomasAndrews Why are you saying that? and even though the factor itself is wrong, the problem is calculating the integral on $\gamma_R$ — Sagigever, May 29 '21 at 15:18
But the integral on $\nu_R$ is the same, as $R\to\infty,$ and $\lim_{R\to\infty}\int_{\eta_R}$ is a known integral. — Thomas Andrews, May 29 '21 at 15:30

score 2 · Accepted Answer · answered May 29 '21 at 15:37

Write the integral as $$\mathfrak{I}\int e^{-(1-i)z^2}\,\mathrm{d}z.$$ As already pointed out in the comments, the integral (without the imaginary part) has been already calculated here and is equal to $\frac12 e^{i \pi/8} \sqrt{\frac{\pi}{\sqrt{2}}}$. Taking the imaginary part yields $$\mathfrak{I}(\frac12 e^{i \pi/8} \sqrt{\frac{\pi}{\sqrt{2}}})=\frac{\sqrt{\pi}}{2} \frac{\sin{(\pi/8)}}{2^{1/4}}=\frac{\sqrt{\pi}}{4} \sqrt{\sqrt{2}-1}.$$

calculate $\int_{0}^{\infty} e^{-t^{2}} \sin \left(t^{2}\right) d t$ by residue theorem

1 Answers1