1

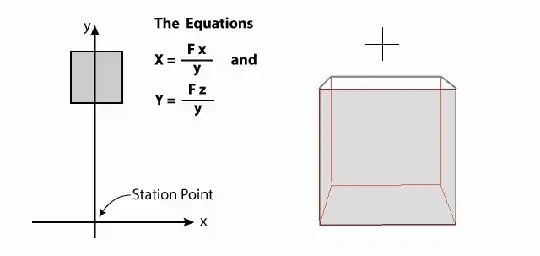
Is anyone familiar with these equations? Please, let me know. 3D Projection Equations

Dhirgham Murran
  • 81
  • 1
    Given a unit vector $u$ the matrix $uu^T$ will be the orthogonal projection onto the space spanned by $u$. Choose two orthogonal unit vectors in the plane you wish to project onto then project onto each and add the two projected vectors together. – CyclotomicField May 23 '21 at 03:55
  • Wouldn't it be simpler to start from first principles, 3D projection on a 2D plane, instead? Do not use Euler or Tait-Bryan angles; those just veer you off into muddy waters. Basic vector algebra (and a tiny little bit of basic linear algebra) is all you need. For computer graphics, add unit quaternions (versors), or bivectors – they implement the same math, just with a different approach –, and you got all the tools you ever need. – Glärbo May 24 '21 at 11:32
  • For Glarbo. Have you shown any final equations on the page of your link https://math.stackexchange.com/a/2306853/918887. I can't see any results in that link. Also, the tilt angle of the camera defines bird's-eye view or worm's eye view as it appears as three point perspective. This is why I introduced the tilt angle of the camera (n) and a magnification constant (F). There's no research anywhere else to see such easy equations to define any object that involves the tilt angle of the camera. I haven't seen any book that gives me complete analyses for three-point perspective or bird's-eye view – Dhirgham Murran May 25 '21 at 16:29

0 Answers0