21

This is a follow-up to the question How good can a "near-miss" polyomino packing be?.

Let $P$ be the heptomino shown below:

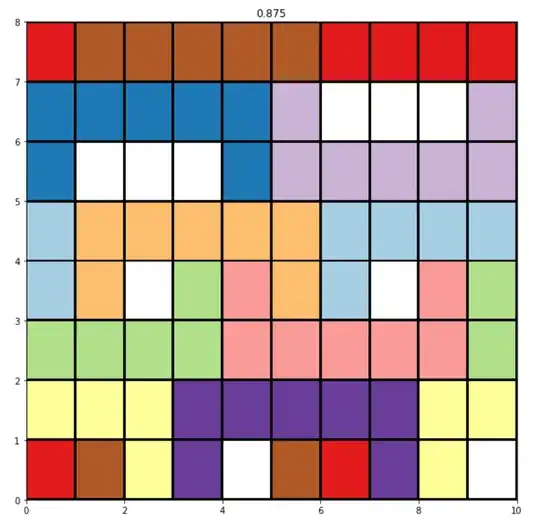
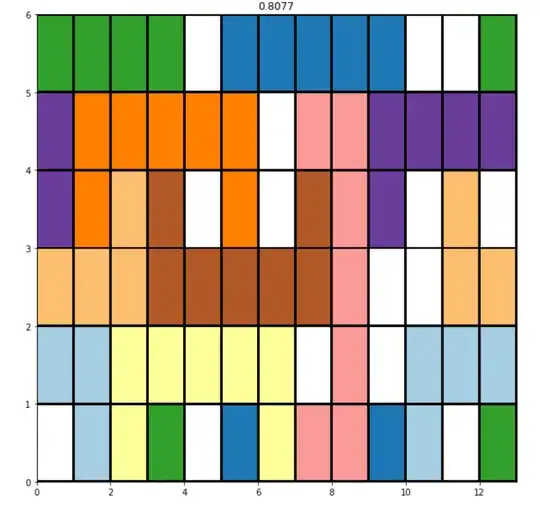
enter image description here

I am interested in the packing density of $P$ on the square grid. (Unlike all polyominoes on $6$ or fewer cells, $P$ does not tile the plane, so by a compactness argument this density must be strictly less than $1$.) The following packing, due to user nickgard here, attains a density of $14/15$:

enter image description here

On the other hand, $P$ cannot cover every cell on the following $65$-cell region, as can be verified by a computer search:

enter image description here

This means that the packing density of $P$ must be at most $64/65$. (Edit: To make this clearer, I've sketched out a more formal argument for why this is the case here.)

How much can we tighten these bounds? There may be smaller regions that $P$ does not cover, but I do not think there will be any size-$15$ ones, so I expect that new techniques will be needed to get an exact answer here.

RavenclawPrefect
  • 18,328
  • 1
    That $65$-cell region doesn't tile the plane, so how does it follow that the packing density is at most $64/65$? – Barry Cipra May 17 '21 at 16:55
  • 1
    @BarryCipra: Choose a "random" position of the $65$-cell region, and then a random cell within it - the resulting distribution is the same as just choosing a random cell from the plane. Since the second step has at most a $64/65$ chance of resulting in a filled-in cell regardless of the position of the region, the odds that a random cell in the plane is filled must be at most $64/65$. (Of course, there isn't really a uniform distribution on $\mathbb{Z}^2$, but insert limits and $N\times N$ squares as necessary to make this rigorous.) – RavenclawPrefect May 17 '21 at 16:59
  • Raven, thanks. There's something in that argument that doesn't seem quite right, but I'll have to give it more thought. The obvious often eludes me. – Barry Cipra May 17 '21 at 17:10
  • 1
    @RavenclawPrefect Let $X$ be the $2 \times 5$ rectangle with an extra square added at a corner. It's not obvious to me how the $64/65$ argument is different from "$P$ cannot cover $X$, so the packing density must be at most $10/11$". Which is incorrect, or course, since you have a packing with density $14/15 \gt 10/11$. – dxiv May 18 '21 at 04:03
  • 1
    @dxiv: But it is possible for $P$ to cover $X$ - $P$ can even cover a $10\times 10$ square, as shown here. – RavenclawPrefect May 18 '21 at 04:54
  • 1
    @RavenclawPrefect I see, thanks. Still, there is something not entirely satisfying in the argument about "choose a "random" position of the 65-cell region, and then a random cell within it". This would be obvious if either (a) the region were tileable, or (b) the "holes" in the optimal cover were known to be randomly placed. However, neither applies here. With that, I am not saying that the argument is wrong, just that it's not all that obvious. – dxiv May 18 '21 at 05:45
  • @dxiv: Thanks for the feedback! I've linked to a more formal argument in the main post, in the hopes of making things clearer - let me know if there are parts that still seem to need justification. – RavenclawPrefect May 18 '21 at 06:29
  • @RavenclawPrefect Thanks, I appreciate. Like someone put it, I'll have to give it more thought. – dxiv May 18 '21 at 06:44

1 Answers1

1

Only a partial answer, but will hopefully spur discussion. I ran a heuristic search algorithm that tries to maximize the density over a rectangle of a fixed size with periodic boundary conditions. (Of course, tiling such a rectangle is sufficient to tile the plane, but this excludes any potential aperiodic tilings). The algorithm did recover the 14/15 tiling but did not find any better ones. Two tilings found by the algorithm are shown below, together with their densities. The first one shown is the second-best tiling after the 14/15 one, although it is rather uninteresting in that it it just several copies of that tiling stuck on top of each other, with rows 2 and 3 breaking the pattern. The second one is the best tiling that did not look like an obvious ``rip off" of the 14/15 one, although parts of it still strongly resemble that one.

The algorithm is very simple and I imagine could be improved considerably. Starting from a fixed tiling, it generates a number of new candidate tilings and then updates to the best among the candidate tilings (best in the sense of covering the greatest number of squares). To encourage exploration, there is also a small chance that at any step it will select a random candidate instead. To generate the candidates, I remove up to two randomly-selected tiles, and then try to add in up to two tiles in different locations or in different orientations than the removed tiles.

The real difficulty seems to be how to sample the candidates in a good way. As far as I can tell the large and irregular shape of the tiles means that there isn't an obvious way to locally modify a tiling to get another tiling. If there were, then I imagine that MCMC (or the heuristic algorithm above) would work quite well. So if you already have a pretty dense tiling, then it will be hard to move to a very dense tiling without some violent transformation of the tiling, making it difficult to explore the space of tilings.

enter image description here enter image description here

Simon Segert
  • 5,819
  • 11
  • 22
  • 1
    Note that the packing shown is just two width-$3$ columns of the $14/15$ density, and one width-$2$ column of density $0.7$. I agree with you that this sort of local manipulation is pretty unlikely to stumble on anything dense - the boundary conditions force any small number of leftover tiles to be in pretty specific arrangements. (For what it's worth, I would be surprised if anything beat the $14/15$ packing - I think the difficulty in this problem lies in finding improvements to the upper bound.) – RavenclawPrefect May 28 '21 at 01:21