For a work we need to evaluate the following integral $$\int_{0}^{1}\frac{\log\left(x\right)}{\sqrt{1+x^{4}}}dx=\,-_{3}F_{2}\left(\frac{1}{4},\frac{1}{4},\frac{1}{2};\frac{5}{4},\frac{5}{4};-1\right).\tag{1}$$ Classical approaches seem to lead nowhere, but it is possible to translating the problem into the language of elliptic functions. Let $\text{sn}(u,k)$ be the Jacobi elliptic sine. We can prove that the evaluation of $(1)$ boils down to the evaluation of $$\int_{0}^{T/4}\log\left(-e^{-\pi i/4}\text{sn}\left(e^{3\pi i/4}z,-1\right)\right)dz$$ where $T=2K(1/2)$ and $K\equiv K(k)$ is the complete elliptic integral of the first kind with $k$ the elliptic modulus. I am not an expert in elliptic functions so I have difficulty to understand if this integral can be evaluated or not. However, I found this formula $$\log\left(\text{sn}\left(u,k\right)\right)=\log\left(\frac{2K}{\pi}\right)+\log\left(\sin\left(\frac{\pi u}{2K}\right)\right)-4\sum_{n\geq1}\frac{1}{n}\frac{q^{n}}{1+q^{n}}\sin^{2}\left(\frac{n\pi u}{2K}\right)$$ with $$q\equiv e^{-\pi\frac{K}{K^{\prime}}}=e^{\pi i\tau}$$ and $\left|\text{Im}\left(\frac{\pi u}{2K}\right)\right|<\frac{\pi}{2}\text{Im}\left(\tau\right)$. So, assuming that we can exchange the integral with the series, which I'm not sure about, the problem boils down to studying the following Lambert series $$\sum_{n\geq1}\frac{1}{n^{2}}\frac{q^{n}}{1+q^{n}}\sin\left(\frac{\pi nT}{4K}\right).\tag{2}$$ I have seen that similar series have been studied but this particular one has not (as far as I know). Clearly, there are a lot of heuristic passages and so I may have written nonsense.
Questions:
$1)$ Is it possible to find a closed form (in terms of special functions) of $(1)$?
$2)$ Assuming that the “elliptic approach” is correct, is there a closed form of $(2)$, maybe in terms of elliptic functions?
Thank you.
Update: The approach used by achille hui in a series of answers (see 1, 2) maybe can be helpful, even if I'm not sure about it.
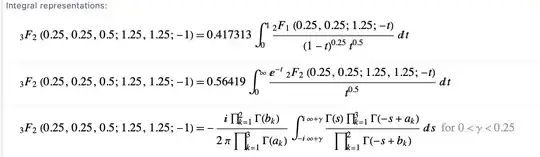
$$\int_{0}^{1}\frac{\log\left(x\right)}{\sqrt{1+x^{4}}}dx=\frac{1}{e^{-i \pi/4}}\int_0^1 \frac{F\left(\left.i \sinh ^{-1}\left(y, e^{i \pi /4}\right)\right|-1\right)}{y} , dy$$
where $F(\phi |m)$ is elliptic integral of the first kind.
I don't understand (using a substitution for example) how this integral form can be transformed into an integral of the form you desire.
– James Arathoon May 13 '21 at 23:12$$\sum_{n\geq 1} \frac{\sec n\pi\frac{1+i}{2}}{n^2} \qquad \sum_{m\in \mathbb{Z}+1/2} \frac{(-1)^{m-1/2}\cot (1+i)m\pi}{m^2}\qquad \sum_{m,n\in \mathbb{Z}}' \frac{i^{m-n}}{n(m^2+n^2)}$$ these series are all equally intractable. In fact, I found the last series being representable as a $_3F_2$ quite surprising.
– pisco May 18 '21 at 10:39