5

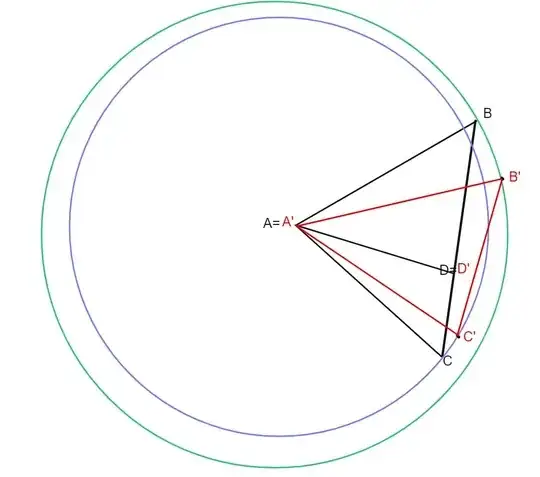
In $\triangle ABC$ and $\triangle A'B'C'$, $D$ is a point on line segment $BC$ and $D'$ is a point on line segment $B'C'$. $\frac{\angle BAD}{\angle CAD}=\frac{\angle B'A'D'}{\angle C'A'D'}$, $AB=A'B'$, $AC=A'C'$ and $AD=A'D'$. How to prove that $\triangle ABC \cong \triangle A'B'C'$?

If $AD$ and $A'D'$ are angle bisectors, the question is much easier: $BD:CD=B'D':C'D'$(angle bisector theorem), then $\triangle ABC \cong \triangle A'B'C'$ is proved by constructing a pair of similar triangles. But I'm stuck on the general question for days.

sputnik
  • 161
Dinshey
  • 555

1 Answers1

0

I'm not sure how formal a proof you want, but I'll show you what I came up with.

  • Draw triangle $ABC$.
  • WLOG, let $A'$ have the same position as $A$ and $D'$ the same position as $D$ (using $\ A'D' = AD$).
  • Try different positions of $B'$ and $C'$ using: $1)\ A'B' = AB,\ 2)\ A'C' = AC$ and $3)\ \angle BAD:\angle CAD=\angle B'A'D':\angle C'A'D'.$

For example, Suppose $\angle B'A'D' < \angle BAD,\ $ that is, $\exists \gamma \in\ [0,1)$ such that $\angle B'A'D' = \gamma (\angle BAD)$. Then $\angle D'A'C' = \gamma (\angle DAC)$. But $D'$ is a fixed point (by assumption) and we see it is not on the line $B'C'$.

The green circle has centre $A$ and passes through $B$ and $B'$. The blue circle has centre $A$ and passes through $C$ and $C'$.

enter image description here

You can use a similar argument for $\angle B'A'D' > \angle BAD.$

Adam Rubinson
  • 24,300