Here is the question. It states:
A circle of radius 1 unit touches positive x -axis and positive y -axis at A and B respectively. A variable line passing through origin intersects the circle in two points D and E . If the area of the triangle DEB is maximum when the slope of the line is $m$ , then the value of $\frac{1}{m^2}$ is
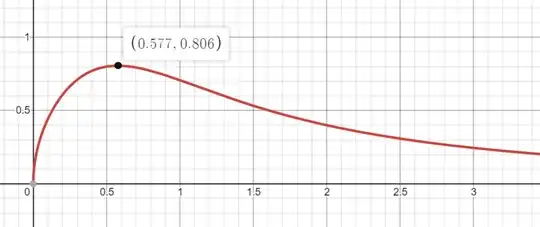
When I tried plotting its graph it came out to be something like this:
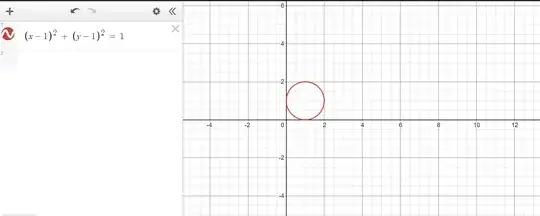
Now When I thought, I Felt like the triangle with maximum area should be an equilateral triangle. So from the center of the circle I joined a line to B which makes 90 with the x axis. This line should also bisect the angle of the equilateral triangle so formed. Hence If I assume point D to be the point intersecting the circle on left. Then the line DB should have a slope $\tan(120) = -\sqrt{3}$. This line shall make and angle 60 with the line DE, so I calculated that and the slope comes out to be $m = 0$
However the answer to $\frac{1}{m^2}$ is $3$ and I am not able to understand how. Any hint/suggestions are appreciated. Thanks for your time
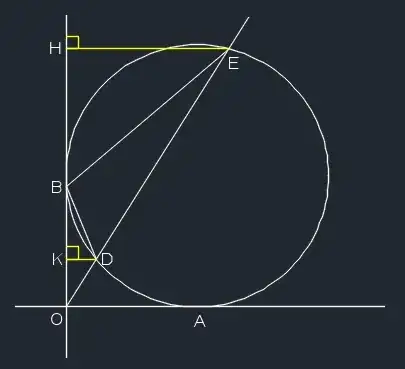
$S_{\triangle BDE}=S_{\triangle BOE}-S_{\triangle BOD}=\frac{1}{2}OB\cdot(X_E-X_D)=\frac{1}{2}(X_E-X_D)$.
If we can express $X_D$ and $X_E$ in terms of slope m, we can find and minimize $S_{\triangle BDE}$.
– Star Bright Apr 16 '21 at 19:53