0

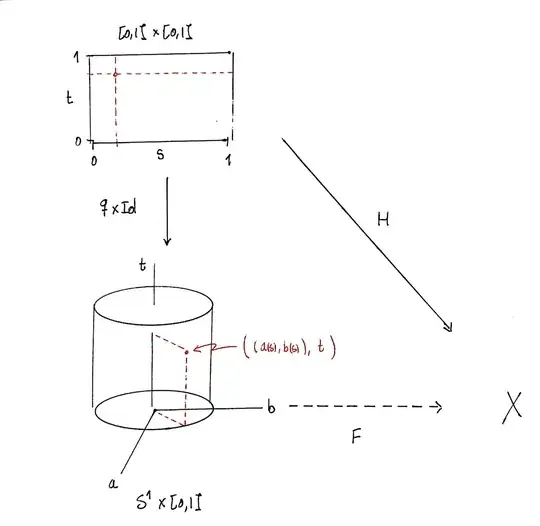
I need to prove the following proposition:

Let $X$ be a path connected topological space. Let $\varphi \colon \mathbb{S}^1 \subset \mathbb{R}^2 \to X$ be a continuous function and $\psi \colon [0, 1] \to X,\ s \mapsto \varphi(\cos2\pi s, \sin2\pi s)$. Then $\varphi$ is homotopic to a constant map if, and only if, $\psi$ is path homotopic to a constant path.

Here is what I have so far:

Denote $x_0 := \varphi(1, 0) \in X$. It is convenient to introduce the maps $\ell$ and $\alpha_0$, in addition to those given in the statement: \begin{align*} \ell &\colon [0, 1] \to \mathbb{S}^1,\ s \mapsto (\cos2\pi s, \sin2\pi s) \\ \alpha_0 &\colon \mathbb{S}^1 \to X,\ (a, b) \mapsto x_0 \\ \varphi &\colon \mathbb{S}^1 \to X,\ (a, b) \mapsto \varphi(a, b) \\ \psi = \varphi \circ \ell &\colon [0, 1] \to X,\ s \mapsto \varphi(\cos2\pi s, \sin2\pi s) \end{align*} being all continuous maps.

  1. ($\Rightarrow$) Suppose $\varphi$ is homotopic to a constant map $\alpha'_0 \colon \mathbb{S}^1 \to X,\ (a, b) \mapsto x'_0$ for some $x'_0 \in X$. Then the constant maps $\alpha'_0$ and $\alpha_0$ are homotopic. By hypothesis $\varphi \simeq \alpha'_0$ and so by transitivity $\varphi \simeq \alpha_0$. Now, using the fact that $\ell \simeq \ell$, we have that $\varphi \circ \ell \simeq \alpha_0 \circ \ell$. But the left-hand side map is just $\varphi \circ \ell = \psi$ while the right-hand side correspond to $(\alpha_0 \circ \ell)(s) = \alpha_0(\ell(s)) = x_0$. Therefore, $\psi$ is homotopic to the constant map $\alpha_0$. Moreover, \begin{align*} \psi(0) = (\varphi \circ \ell)(0) = \varphi(\ell(0)) \varphi(1, 0) = x_0 \quad \text{and} \quad (\alpha_0 \circ \ell)(0) = \alpha_0(\ell(0)) = x_0 \\ \psi(1) = (\varphi \circ \ell)(1) = \varphi(\ell(1)) \varphi(1, 0) = x_0 \quad \text{and} \quad (\alpha_0 \circ \ell)(1) = \alpha_0(\ell(1)) = x_0 \end{align*} so both paths are path homotopic.

But I'm stuck in the ($\Leftarrow$)-direction. Can you help me with hints on how to proceed in this direction?

SNC92
  • 43

1 Answers1

0

Suppose $\psi$ is path homotopic to a constant path $\gamma_0 \colon [0, 1] \to X,\ s \mapsto x_0$ for $x_0 \in X$, i.e. there exists a homotopy $H \colon [0, 1] \times [0, 1] \to X$ such that $H(s, 0) = \psi(s)$ and $H(s, 1) = x_0$. Note that the map $\ell$ is continuous, surjective, and closed, so it is a quotient map. Consider now the function \begin{equation} \ell \times \text{Id} \colon [0, 1] \times [0, 1] \to \mathbb{S}^1 \times [0, 1],\ (s, t) \mapsto (\ell(s), t) \end{equation} which also corresponds to a quotient map. Indeed:

  1. The component functions $(s, t) \mapsto \ell(t)$ and $(s, t) \mapsto t$ are continuous, so it is $(s, t) \mapsto (\ell(t), t)$;
  2. Let $((a, b), t) \in \mathbb{S}^1 \times [0, 1]$. Consider the point $(s, t) \in [0, 1] \times [0, 1]$ with $s \in [0, 1]$ such that $\ell(s) = (a, b)$ (such $s$ is guaranteed since $\ell$ is surjective). Then $(\ell \times \text{Id})(s, t) = ((a, b), t)$;
  3. Let $C = A \times B \subset \mathbb{S}^1 \times [0, 1]$ be a closed subset (with $A$ and $B$ being closed in $\mathbb{S}^1$ and $[0, 1]$, respectively). Then $(\ell \times \text{Id})(C) = \ell(C) \times B$ which is closed in $[0, 1] \times [0, 1]$ (remember that $\ell$ is a closed map). Therefore, $\ell \times \text{Id}$ is a closed map as well.

Now we are going to use Theorem $22.2$ [Topology, J.~R.~Munkres (2nd Edition)]. Let let us analyze the fiber of each element $\mathbb{S}^1 \times [0, 1]$ under $\ell \times \text{Id}$. We have $2$ cases:

  1. If $((a, b), t) \neq ((1, 0), t)$ we have \begin{equation} (\ell \times \text{Id})^{-1}(\{((a, b), t)\}) = \{(s, t)\} \end{equation} and so $H$ is (trivially) constant in each of these fibers;
  2. If $((a, b), t) = ((1, 0), t)$ with $t \in [0, 1]$, then \begin{equation} (\ell \times \text{Id})^{-1}(\{((1, 0), t)\}) = \{(0, t), (1, t)\} \end{equation} But $H(0, t) = x_0$ and $H(1, t) = x_0$ so $H$ is constant over these fibers. Therefore, by theorem $22.2$ there exists a continuous function \begin{equation} F \colon \mathbb{S}^1 \times [0, 1] \to X \end{equation} such that $H = F \circ (\ell \times \text{Id})$, i.e. such that the following figure commutes:

enter image description here

We claim that the function $F$ corresponds to a homotopy between $\varphi$ and the constant map $(a, b) \mapsto x_0$. Indeed, first note that, explicitly, we have \begin{equation} H(s, t) = F\bigl((a(s), b(s)), t\bigr) \end{equation} where $s \in [0, 1]$ is such that $\ell(s) = (a, b)$ (note this equation is well-defined even for $s \in \{0, 1\}$). Then,

  1. On the one hand, if $s \in ]0, 1[$ then $\ell(s) = (a, b) \neq (1, 0)$ and the quotient map $\ell$ is bijective in such restricted domain; then we have \begin{equation} F\bigl((a, b), 0\bigr) = H(s, 0) = \psi(s) = (\varphi \circ \ell)(\ell^{-1}(a, b)) = \varphi(a, b) \end{equation} On the other hand, if $s \in \{0, 1\}$ then $\ell(s) = (a, b) = (1, 0)$ and we have \begin{equation} F\bigl((1, 0), 0\bigr) = \begin{cases} H(0, 0) = \psi(0) = \varphi(\ell(0)) = \varphi(1, 0) \\ H(1, 0) = \psi(1) = \varphi(\ell(1)) = \varphi(1, 0) \end{cases} \end{equation} and so $F\bigl((1, 0), 0\bigr)$ is well-defined. Putting all the cases together, we get that $F\bigl((a, b), 0\bigr) = \varphi(a, b)$.
  2. $F\bigl((a, b), 1\bigr) = H(s, 1) = x_0$

Therefore, $F$ corresponds to a homotopy between $\varphi$ and $s \mapsto x_0$.

SNC92
  • 43