6

Let $X_1,X_2,\dots,X_n$ be i.i.d observations of a continuous random variable $X$. Let $Y_n$ be the sample variance: $$ Y_n = \bigg(n\sum_{i=1}^n X_i^2 - \bigg(\sum_{i=1}^nX_i \bigg)^2\bigg)^k. $$ Actually, for $k=1$, $Y_n$ is simply the sample variance scaled by $n^2$, i.e., we can write it as $$ Y_n = n^2 \bigg(\frac{1}{n}\sum_{i=1}^n X_i^2 - \bigg(\frac{1}{n}\sum_{i=1}^nX_i \bigg)^2\bigg). $$

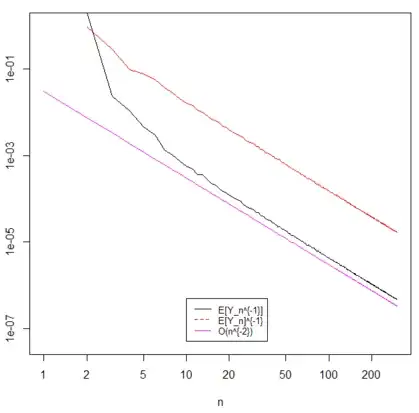
Here is a plot for the case of $k=1$.

enter image description here

From running computational simulations it is clear that $E[Y_n^{-1}]$ and $E[Y_n]^{-1}$ converge at the same rate as $n \to \infty$, e.g. there exists constants $C_1$ and $C_2$ such that $$ C_1 E[Y_n]^{-1} \le E[Y_n^{-1}] \le C_2 E[Y_n]^{-1}, $$ for some constant $C$. In fact the simulations show they both converge as $O(n^{-2k})$. But how can we prove they have the same rate of convergence?

sonicboom
  • 10,273
  • 15
  • 54
  • 87

1 Answers1

1

For $k=1,$ we write $Y_n = n^2 S_n^2$ in the standard notation. Now, just forget about $n^{-2}$ (it will occur as it is in both $E[Y_n^{-1}]$ and $E[Y_n]^{-1}$). The rest should follow by applying Delta method with $g(x) = 1/x$ on the large sample CLT for $S_n^2$ which states that $\sqrt{n}(S_n^2 - E[S_n^2])$ converges in distribution to $N(0, \tau^2)$ for some $\tau^2>0.$

The same method should also work for any general $k.$

Fill in the details.

Aditya Ghosh
  • 1,232