In Greg Friedman's article "An elementary illustrated introduction to simplicial sets" (2016), there is the following definition:
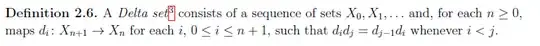
Given such a Delta set $X$, we can form a chain complex $C_\ast(X)$ by defining $C_n(X)$ to be the free abelian group generated by $X_n$ and $$\partial_n := \sum_{i=0}^{n} (-1)^i\, d_i: C_n(X)\to C_{n-1}(X).$$
Is the corresponding homology isomorphic to the singular homology of the geometric realization $|X|$ of $X$, defined as $$ |X| := \Big( \bigsqcup_{n=0}^\infty (X_n\times\Delta^n) \Big) \Big/ \sim $$ where $\sim$ is the equivalence relation generated by $(x,(t_0,\dots,t_{i-1},0,t_{i+1},\dots,t_{n-1}))\sim (d_i(x),(t_0,\dots,t_{n-1}))$?
I know that this is true if $X$ is a simplicial set. But what about the case of a Delta set? If it is true, does there exist a chain homotopy equivalence between $C_\ast(X)$ as defined above and the singular chain complex $S_\ast(|X|)$ of $|X|$? What about the chain homomorphism $$\theta: C_\ast(X)\to S_\ast(|X|)$$ defined on a generator $x\in X_n$ of $C_n(X)$ by $$\theta(x) := (t\to [x,t])\in S_n(|X|)?$$
Or would it be perhaps easier to use the cellular chain complex?
Any help is much appreciated. Thank you in advance!