Area of $(x-3)^2+(y+2)^2<25: (x,y) \in L_1 \cap L_2$

Question

Two lines $(L_1,L_2)$ intersects the circle $(x-3)^2+(y+2)^2=25$ at the points $(P,Q)$ and $(R,S)$ respectively. The midpoint of the line segment $PQ$ has $x$-coordinate $-\dfrac{3}{5}$, and the midpoint of the line segment $RS$ has $y$-coordinate $-\dfrac{3}{5}$.

If $A$ is the locus of the intersections of the line segments $PQ$ and $RS$, then the area of the region $A$ is:

---

What I've done:

Consider $L_1: y= ax+b$. The midpoint of the chord $PQ$ is $(-\dfrac{3}{5}, -\dfrac{3a}{5}+b)$. Now, using the property that the midpoint of a chord of a circle and the center of the circle $(3,-2)$ are perpendicular we have: $\dfrac{-\dfrac{3a}{5}+b-(-2)}{-\dfrac{3}{5}-(3)} *a = -1$ $$\implies b= \dfrac{3a^2-10a+18}{5a}$$ This means we can eliminate one variable and write the equation of $L_1: y= ax+ \dfrac{3a^2-10a+18}{5a}$

From this form of $L_1$ we can get the value of the minimum value of the $y$-intercept by differentiating $b$. Let $b= f(a) = \dfrac{3a^2-10a+18}{5a}, f'(a) = \dfrac{3a^2-18}{5a^2}, f'(a)=0 \implies a = \pm \sqrt{6}$. I just found this hoping we will get bounds on the y-intercept of $L_1$.

Now lets do the same process for $L_2$.

Consider $L_2: y= cx+d$. The midpoint of the chord $RS$ is $(\dfrac{-\dfrac{3}{5} -d}{c},-\dfrac{3}{5})$. Now, using the property that the midpoint of a chord of a circle and the center of the circle $(3,-2)$ are perpendicular we have: $\dfrac{-\dfrac{3}{5}+2}{\dfrac{-\dfrac{3}{5} -d}{c}-3} *c = -1$ $$\implies d= \dfrac{7c^2-15c-3}{5}$$ This means we can eliminate one variable and write the equation of $L_2: y= cx+ \dfrac{7c^2-15c-3}{5}$

From this form of $L_2$ we can get the value of the minimum value of the $y$-intercept by differentiating $d$. Let $d= f(c) = \dfrac{7c^2-15c-3}{5}, f'(c) = \dfrac{14c-15}{5}, f'(c)=0 \implies c = \dfrac{15}{14}$. I just found this hoping we will get bounds on the y-intercept of $L_2$.

Along with all this, we can set bounds when the line segment is just about to leave the circle (tangent to the circle).

What I can visualize:

Let $X$ = union of all line segments $PQ$. Let $Y$ = union of all line segments $RS$. Every point in the intersection of $X$ and $Y$ is a candidate intersection point of the lines $L_1$ and $L_2$. So A = $X \cap Y$

Edit 1: I saw the equation of $L_1$ varying as $a$ varies on DESMOS and think the boundry of the union of all line segments PQ might be an outer circle.

Answer 1

EDIT (Original answer at the end).

I want to show how the envelope of chords $RS$ (or $PQ$) can be obtained without calculus and without coordinates (see figure below).

Let's start with a chord $AB$ of a circle of centre $O$. For any point $M$ on that chord, we can construct a line $RS$ passing through $M$ and perpendicular to $OM$. We want to find the envelope of all those lines, i.e. the curve which is tangent to all the lines $RS$ as $M$ varies on $AB$.

Consider then another point $M'$ on $AB$ and its associated line $R'S'$. Let $P$ be the intersection of $RS$ and $R'S'$, $T$ the tangency point of $RS$ with the envelope, $T'$ the tangency point of $R'S'$ with the envelope. As $M'$ approaches $M$, both $T'$ and $P$ approach $T$.

But the circle through $OMM'$ also passes through $P$ (because $\angle PMO=\angle PM'O=90°$) and this circle, as $M'\to M$, tends to the circle through $O$ tangent to $AB$ at $M$. Hence $T$, which is the limiting position of $P$, is the intersection of that circle with line $RS$. Moreover, $OT$ is a diameter of that circle.

Now that we know how to construct point $T$ on $RS$, let's also construct line $HK$, parallel to $AB$ at a distance from it equal to the distance of $O$ from $AB$. If $J$ is the projection of $T$ on it, then $TJ=TO$, because line $CH$ joining the midpoints of the legs of a trapezoid is the arithmetic mean of bases $OK$ and $TJ$.

It follows that point $T$ has the same distance from $O$ and from line $HK$. Hence its locus (which is the envelope) is a parabola, having $O$ as focus and $HK$ as directrix.

ORIGINAL ANSWER.

What you need is the envelope $\gamma_1$ formed by lines $L_1$ and the envelope $\gamma_2$ formed by lines $L_2$.

As the equation of $L_1$ is $y=\left(x+{3\over5}\right)a-2+{18\over5a}$, differentiating w.r.t. $a$ we get: $x+{3\over5}-{18\over5a^2}=0$, which can be solved for $a$: $$ a^2={18\over 5x+3}. $$ Inserting this into the equation of $L_1$ we get (after some algebra): $$ 25(2+y)^2={72}(5x+3), $$ which is the desired envelope $\gamma_1$ (a parabola).

Repeating the same process for $L_2$ we can find the equation of $\gamma_2$ (another parabola): $$ y=-{5\over28}(3-x)^2-{3\over5}. $$ Lines $L_1$ and $L_2$ are tangent to their envelope, hence the area you want to compute is that external to both parabolas but inside the circle.

To compute the area, one has to find the coordinates of the upper intersection $A$ between $\gamma_1$ and the circle, of the left intersection $C$ between $\gamma_2$ and the circle and of the intersection $B$ between $\gamma_1$ and $\gamma_2$ lying inside the circle: $$ A=\left(\frac{4}{5},\frac{6}{5} \sqrt{14}-2\right),\quad C=\left(3-\frac{6}{5}\sqrt{14},-\frac{21}{5}\right),\quad B=\left(\frac{1}{5} \left(29-12 \sqrt{7}\right),\frac{2}{5} \left(6 \sqrt{7}-23\right)\right). $$

Integrating along $y$ the area can then be computed as: $$ \begin{align} area&=\int_{y_B}^{y_A} \left[\left(\frac{5}{72}(y+2)^2-\frac{3}{5}\right)-\left(3-\sqrt{25-(y+2)^2}\right)\right] \, dy \\ &+\int_{y_C}^{y_B} \left[\left(-\frac{2}{5} \sqrt{-35 y-21}+3\right)-\left(3-\sqrt{25-(y+2)^2}\right)\right] \, dy \\ &=\frac{25 \pi }{4}+4 \sqrt{14 \left(9-4 \sqrt{2}\right)}-\frac{3004}{75}. \end{align} $$

Answer 2

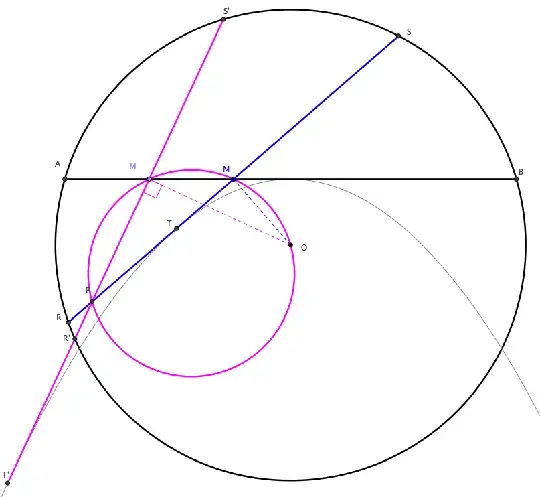
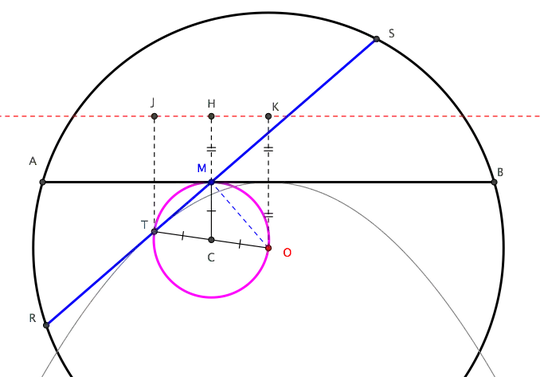
Before one attempts to solve this problem one must visualize this:

Let $U$ = union of all lines $L_1$. Let $V$ = union of all lines $L_2$. Every point in the region $U \cap V$ is a candidate intersection point of the lines $L_1$ and $L_2$. Therefore, $L = U \cap V$ such that the intersection point lies inside the circle.

Some Facts: Further information

1. $y = mx + \dfrac{a}{m}$ is a tangent to the parabola $y^2 = 4ax$, whatever be the value of $m$.

2. $y = mx -am^2$ is a tangent to the parabola $x^2 = 4ay$, whatever be the value of $m$.

3. For any point $P$, that is outside a parabola, there is at least one tangent on the parabola passing through $P$.

Study the set of lines $L_1$:

Consider $L_1: y= ax+b$. The midpoint of the chord $PQ$ is $(-\dfrac{3}{5}, -\dfrac{3a}{5}+b)$. Now, using the property that the midpoint of a chord of a circle and the center of the circle $(3,-2)$ are perpendicular we have: $\dfrac{-\dfrac{3a}{5}+b-(-2)}{-\dfrac{3}{5}-(3)} *a = -1$ $$\implies b= \dfrac{3a^2-10a+18}{5a} = \dfrac{3a}{5} -2 + \dfrac{18}{5a}$$ This means we can eliminate one variable and write the equation of $L_1: y= ax+ \dfrac{3a^2-10a+18}{5a}$ for all $a$.

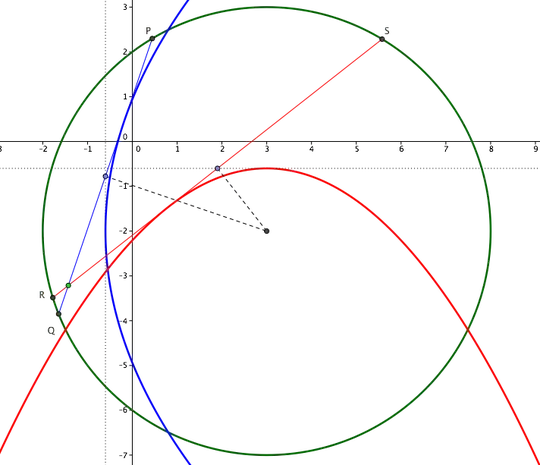
$L_1: y+2= a(x+ \dfrac{3}{5})+\dfrac{18}{5a}$. Let $Y = y+2, X = x+ \dfrac{3}{5} \implies Y = aX + \dfrac{18}{5a}$. Using fact 1, we get that $L_1$ is always tangent to parabola: $Y^2 = \dfrac{72X}{5}$. Upon back substitution, we get: $(y+2)^2 = \dfrac{72(x+ \dfrac{3}{5})}{5} \implies 25(y+2)^2 = 72(5x+3)$. So in conclusion the set of lines $L_1$ are just the set of all tangents to this parabola: ($P_1$). Using fact 3, for any point that is outside $P_1$, a tangent line from $P_1$ can be drawn to that point. Hence union of all tangents is the region outside $P_1$.

Study the set of lines $L_2$:

Consider $L_2: y= cx+d$. The midpoint of the chord $RS$ is $(\dfrac{-\dfrac{3}{5} -d}{c},-\dfrac{3}{5})$. Now, using the property that the midpoint of a chord of a circle and the center of the circle $(3,-2)$ are perpendicular we have: $\dfrac{-\dfrac{3}{5}+2}{\dfrac{-\dfrac{3}{5} -d}{c}-3} *c = -1$ $$\implies d= \dfrac{7c^2-15c-3}{5} = \dfrac{7c^2}{5} - 5c - \dfrac{3}{5} $$ This means we can eliminate one variable and write the equation of $L_2: y= cx+ \dfrac{7c^2-15c-3}{5}$ for all $c$.

$L_2: y+ \dfrac{3}{5}= c(x- 3)+\dfrac{7c^2}{5}$. Let $Y = y+ \dfrac{3}{5}, X = x- 3\implies Y = cX + \dfrac{7c^2}{5}$. Using fact 2, we get that $L_2$ is always tangent to parabola: $X^2 = -\dfrac{28Y}{5}$. Upon back substitution, we get: $(X-3)^2 = -\dfrac{28(y+ \dfrac{3}{5})}{5} \implies y= \dfrac{-5(x-3)^2}{28} - \dfrac{3}{5} (P_2)$.

So overall, for any point outside both $P_1$ and $P_2$ a tangent can be drawn to both $P_1$ and $P_2$ from that point, so the locus of intersection points of $L_1$ and $L_2$ is any point outside both the parabolas. But we must remember that the intersection point must be inside the circle because we are looking for the locus of the intersection of the chords $PQ$ and $RS$, both of which must reside inside the circle, hence their intersection will also be inside the circle. So the region is: $$L: \{(x,y) \in \mathbb{R}: y> \dfrac{-5(x-3)^2}{28} - \dfrac{3}{5}, 25(y+2)^2 > 72(5x+3), (x-3)^2 + (y+2)^2<25 \}$$

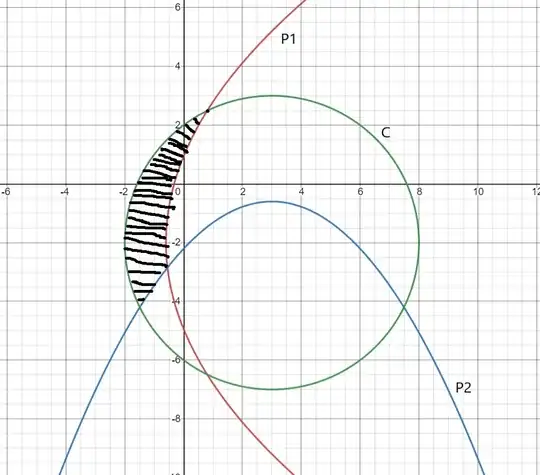
To make finding the area simpler lets shift this region (make the circle have center at origin): $X = x+3, Y = y-2$ $$ \implies L: \{(X,Y) \in \mathbb{R}: Y> \dfrac{-5(X)^2}{28} + \dfrac{7}{5}, 25(y)^2 > 72(5x+18), (x)^2 + (y)^2<25 \}$$

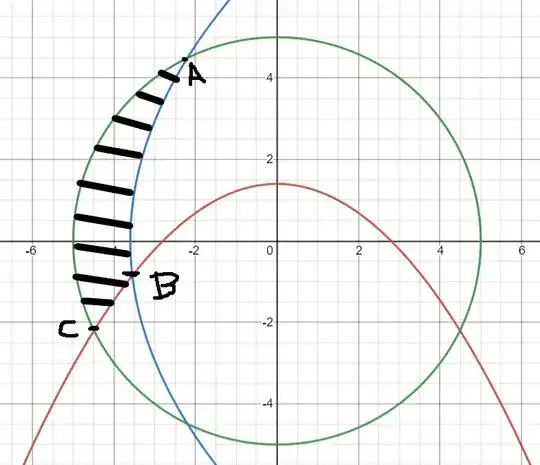$A: \left(- \dfrac{11}{5}, \dfrac{6\sqrt{14}}{5}\right); B: \left(-\dfrac{2(6\sqrt{7}-7)}{5}, - \dfrac{12(\sqrt{7}-3)}{5}\right); C: \left(-\dfrac{6\sqrt{14}}{5}, - \dfrac{11}{5}\right) $ .

The longest distance $d$ between any two points in the region is obviously AC because A is the point with both maximum x and y coordinates. Any point on $P_2$ (in the shaded region) is closer to A than C because both the x and y coordinates is closer to A. Also any other point along the circle is a chord and C is farthest away as none of the points is the diameter, hence C is the farthest point from A. $d = AC = \sqrt{50} = 5\sqrt{2}$.

Finding the area is a tedious task to do by hand. It can be computed as follows:

Region above the axis: $\int_{-5}^{-\frac{18}{5}}\sqrt{25-x^{2}}dx+\int_{-\frac{18}{5}}^{-\frac{11}{5}}\left(\sqrt{25-x^{2}} - \sqrt{\frac{72\left(5x+18\right)}{25}} \right)dx$

Region below the axis: $\left|\int_{-5}^{-\frac{6\sqrt{14}}{5}}-\sqrt{25-x^{2}}dx+\int_{-\frac{6\sqrt{14}}{5}}^{-\frac{18}{5}}\left(-\frac{5}{28}\left(x\right)^{2}+\frac{7}{5}\right)dx+\int_{-\frac{18}{5}}^{-\frac{2\left(6\sqrt{7}-7\right)}{5}}\left(\left(-\frac{5}{28}\left(x\right)^{2}+\frac{7}{5}\right)-\left(-\sqrt{\frac{72\left(5x+18\right)}{25}}\right)\right)dx\right|$

Adding both these values we get area of region $= 6.94701 \implies \lfloor{1000*6.94701}\rfloor = \lfloor{6947.01...}\rfloor = 6947$