Synthetic proof that, given points $A,B,C,D$ in space, $\angle BAC \leq \angle BAD+\angle DAC$?

Question

Consider the following statement:

Given points $A,B,C,D$ in space, $\angle BAC \leq \angle BAD+\angle DAC$.

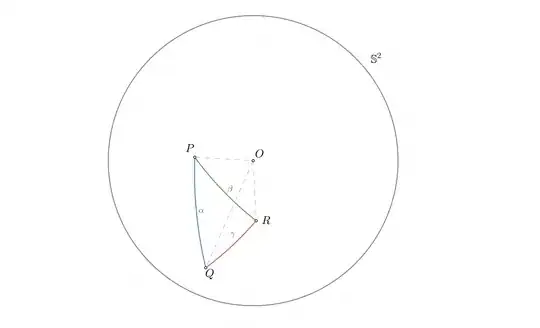
This seems obvious enough -- if you're rotating a beam that moves through space at a fixed angular speed, the fastest way to go from pointing at $B$ to at $C$ is directly, as opposed to through some other point $D$. This is also equivalent to the triangle inequality on a sphere (where the distance between two points on a sphere is defined to be the length of the arc), if we specify $AB=AC=AD=1$.

However, my attempts to find a simple geometric proof have been elusive. It's certainly possible to prove the spherical triangle inequality via the spherical law of cosines, analogously to the proof of the (Euclidean) triangle inequality using the standard law of cosines, but proving this law seems to require assigning coordinates somehow. The calculations aren't that bad, but they seem considerably hairier than such a simple statement should require.

Is there a strictly geometric (synthetic) proof of this result?

Answer 1

There is! And it goes back to Euclid.

Since “lines” in $\mathbb{S}^2$ are great circles, which in turn are unit circles in planes through the origin in $\mathbb{R}^3$, the arc lengths of a spherical triangle $\triangle PQR\subset \mathbb{S}^2$ are the face angles $\alpha,\beta,\gamma$ of a tetrahedral vertex at the origin, as shown in Figure 1.

$$\tag{Fig. 1}$$

Hence, we need only show that the sum of any two face angles of a tetrahedron at a vertex $A$ are greater than the third face angle at $A$. To do this we construct a particular tetrahedron as follows (see Figures $2$ and $3$ below). Take any three lines $\mathscr{L}_1, \mathscr{L}_2,\mathscr{L}_3$ in space that meet at a point $A$. Choose any points $B,C$ on $\mathscr{L}_1, \mathscr{L}_2$ respectively, then construct the point $E$ lying in the plane formed by $\mathscr{L}_2$ and $\mathscr{L}_3$, such that $\lvert AB\rvert=\lvert AE\rvert$ and $\angle CAB=\angle EAC$. Lastly, produce the line $CE$ (if necessary) to meet $\mathscr{L}_3$ at $D$. We will show (Book $11$ Proposition $20$, Euclid's Elements)

For the tetrahedron $\triangle ABCD$, $$\angle CAB \lt \angle DAC +\angle BAD.$$

Proof:

There are two ways to prove this: $1)$ break into cases $\lvert CD\rvert\gt \lvert CE\rvert$ and $\lvert CD\rvert\lt \lvert CE\rvert$, then simply check off angle measures, or $2)$ show $\lvert DE\rvert\lt \lvert BD\rvert$, using the $\mathbb{E}^2$ triangle inequality.

We will prove $(2)$. By our construction $$\triangle ABC\cong\triangle ACE.$$ From the $\mathbb{E}^2$ triangle inequality $$\lvert BC\rvert=\lvert CE\rvert\lt\lvert BD\rvert+\lvert CD\rvert\implies \lvert BD\rvert\gt \big\lvert\lvert CE\rvert-\lvert CD\rvert\big\rvert=\lvert DE\rvert$$ and since $\triangle ABD$ and $\triangle AED$ share a common side $AD$ and $\lvert AB\rvert=\lvert AE\rvert$ we conclude $$\angle DAE\lt\angle BAD.$$ Thus $$\angle CAB=\angle EAC\leq \angle DAC +\angle DAE\lt \angle DAC +\angle BAD.$$ $\square$

$$\tag{Fig. 2}$$

$$\tag{Fig. 3}$$